What Is The Lcm Of 14 And 10
Kalali
Jun 14, 2025 · 3 min read
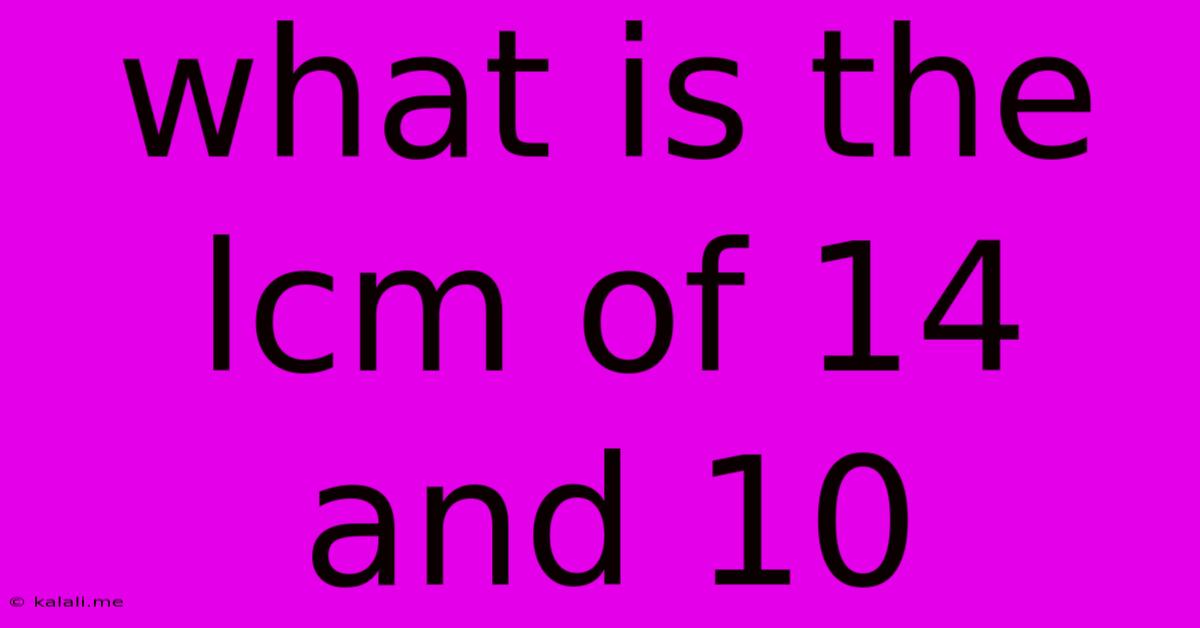
Table of Contents
What is the LCM of 14 and 10? A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, frequently used in various applications, from simplifying fractions to solving complex algebraic equations. This article will clearly explain how to calculate the LCM of 14 and 10, providing different methods to understand the concept fully. Understanding LCM is crucial for anyone studying arithmetic, algebra, or even advanced mathematics. We'll explore the process step-by-step, making it easy for all levels of understanding.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest positive integer that is divisible by both of the given numbers without leaving a remainder. It's the smallest number that is a multiple of both numbers. For instance, multiples of 14 are 14, 28, 42, 56, 70, 84... and multiples of 10 are 10, 20, 30, 40, 50, 60, 70, 80... Notice that 70 appears in both lists; it's the smallest number common to both, making it the LCM.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 14: 14, 28, 42, 56, 70, 84...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80...
As you can see, the smallest number appearing in both lists is 70. Therefore, the LCM of 14 and 10 is 70.
Method 2: Prime Factorization
This method is more efficient for larger numbers. We find the prime factorization of each number, then identify the highest power of each prime factor present in either factorization. The product of these highest powers is the LCM.
- Prime factorization of 14: 2 x 7
- Prime factorization of 10: 2 x 5
The prime factors involved are 2, 5, and 7. The highest power of 2 is 2¹, the highest power of 5 is 5¹, and the highest power of 7 is 7¹.
Therefore, the LCM = 2 x 5 x 7 = 70
Method 3: Using the Formula (LCM and GCD)
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD (greatest common divisor) of 14 and 10. The GCD is the largest number that divides both 14 and 10 without leaving a remainder. In this case, the GCD of 14 and 10 is 2.
Now, we can apply the formula:
LCM(14, 10) = (14 x 10) / 2 = 140 / 2 = 70
Therefore, the LCM of 14 and 10 is 70.
Conclusion
We've explored three different methods to find the LCM of 14 and 10. Regardless of the method used, the answer remains consistent: the LCM of 14 and 10 is 70. Understanding these methods empowers you to tackle similar problems involving larger numbers and strengthens your foundational mathematical skills. Choosing the most appropriate method depends on the complexity of the numbers involved; for smaller numbers, listing multiples is often sufficient, while prime factorization is generally more efficient for larger numbers. Remember that mastering the concept of LCM is essential for further mathematical studies and problem-solving.
Latest Posts
Latest Posts
-
Which Of The Following Is True Of Shaded Pole Motors
Jun 14, 2025
-
All Of The Following Are Examples Of Video Conferencing Systems Except
Jun 14, 2025
-
What Unit Is Used To Measure Wavelength
Jun 14, 2025
-
Points A And B Are 200 Mi Apart
Jun 14, 2025
-
Lcm Of 3 5 And 9
Jun 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 14 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.