What Is The Lcm Of 6 And 12
Kalali
Jul 25, 2025 · 5 min read
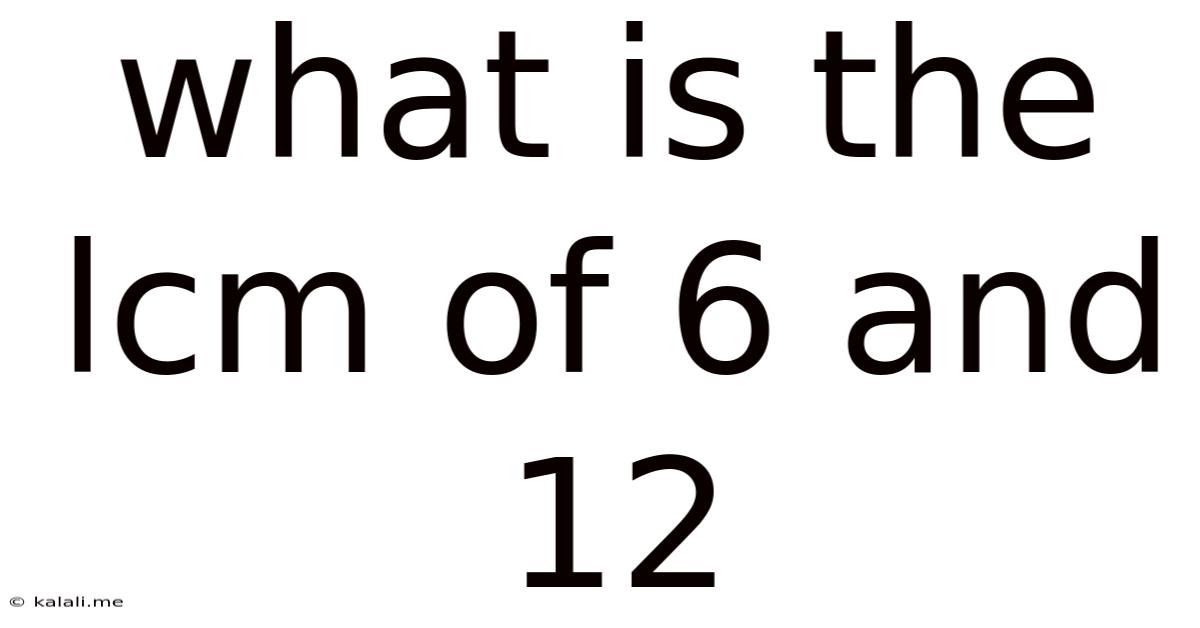
Table of Contents
What is the LCM of 6 and 12? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic problem, but understanding the underlying concepts and various methods for calculating the LCM is crucial for a strong foundation in mathematics. This article will explore the LCM of 6 and 12 in detail, providing multiple approaches to solve this problem and extending the understanding to more complex scenarios. We'll delve into the definition of LCM, explore different calculation methods, discuss the applications of LCM in real-world situations, and even touch upon its relation to the greatest common divisor (GCD). This comprehensive guide will equip you with a thorough understanding of LCM, far beyond just finding the answer for 6 and 12.
Meta Description: This article comprehensively explains how to find the least common multiple (LCM) of 6 and 12, exploring various methods, real-world applications, and its relationship with the greatest common divisor (GCD). Learn more than just the answer; understand the underlying mathematical concepts.
Understanding Least Common Multiples (LCM)
Before we jump into calculating the LCM of 6 and 12, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding this definition is key to grasping the various methods used to calculate the LCM.
For instance, the multiples of 6 are 6, 12, 18, 24, 30, and so on. The multiples of 12 are 12, 24, 36, 48, and so on. Notice that 12 appears in both lists. This is the smallest number that's a multiple of both 6 and 12, making it the LCM.
Methods for Calculating the LCM of 6 and 12
There are several ways to calculate the LCM, each with its own advantages and disadvantages. Let's explore the most common methods:
1. Listing Multiples:
This is the most straightforward method, especially for smaller numbers like 6 and 12. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 12: 12, 24, 36, 48...
As you can see, the smallest number that appears in both lists is 12. Therefore, the LCM of 6 and 12 is 12.
This method is simple and intuitive but becomes less efficient when dealing with larger numbers or more than two numbers.
2. Prime Factorization Method:
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then building the LCM from the prime factors.
- Prime factorization of 6: 2 x 3
- Prime factorization of 12: 2 x 2 x 3 (or 2² x 3)
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
Multiply these highest powers together: 2² x 3 = 4 x 3 = 12. Therefore, the LCM of 6 and 12 is 12.
This method is more systematic and works well for larger numbers and multiple numbers.
3. Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the relationship between the LCM and the greatest common divisor (GCD). The GCD is the largest number that divides both a and b without leaving a remainder.
First, we need to find the GCD of 6 and 12. The factors of 6 are 1, 2, 3, and 6. The factors of 12 are 1, 2, 3, 4, 6, and 12. The greatest common factor is 6.
Now, we can use the formula:
LCM(6, 12) = (6 x 12) / GCD(6, 12) = 72 / 6 = 12
This method is efficient once you know how to calculate the GCD, which can be done using various methods like the Euclidean algorithm.
Understanding the Relationship Between LCM and GCD
The relationship between the LCM and GCD is fundamental in number theory. The formula LCM(a, b) = (|a x b|) / GCD(a, b) highlights this connection. This formula is very useful and efficient for finding the LCM of larger numbers. Understanding this relationship provides a deeper insight into the structure and properties of integers.
Real-World Applications of LCM
The concept of LCM isn't just a theoretical exercise; it has practical applications in various fields:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 6 minutes, and another every 12 minutes. The LCM (12 minutes) tells you when both buses will arrive at the stop simultaneously.
-
Construction: In construction projects, materials might need to be ordered in multiples of specific quantities. Finding the LCM helps determine the least amount of material needed to satisfy all requirements.
-
Music: The LCM is used in music theory to determine the least common denominator for different musical rhythms and tempos.
-
Calendars: Determining when certain events will occur again on the same day of the week can involve finding the LCM of the number of days in a week and the interval between events.
Extending the Concept to More Than Two Numbers
The methods discussed above can be extended to calculate the LCM of more than two numbers. The prime factorization method is particularly useful in such cases. For example, to find the LCM of 6, 12, and 18:
- Prime factorization of 6: 2 x 3
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
The highest powers of the prime factors are 2² and 3². Therefore, the LCM(6, 12, 18) = 2² x 3² = 4 x 9 = 36.
Conclusion: Beyond the Simple Answer
While the LCM of 6 and 12 is simply 12, this article aimed to provide a much deeper understanding of the concept of least common multiples. We explored various calculation methods, highlighted the importance of the relationship between LCM and GCD, and discussed real-world applications. Mastering the LCM is not just about solving a specific problem; it's about building a robust understanding of fundamental mathematical principles that extend far beyond this simple example. This knowledge will serve as a strong foundation for tackling more complex mathematical concepts in the future. Remember that the most efficient method will often depend on the context and the numbers involved. Practice using different methods to solidify your understanding and find the best approach for each scenario.
Latest Posts
Latest Posts
-
Oregon Farms Carrot Cake Where To Buy
Jul 26, 2025
-
How Many Feet In 1 City Block
Jul 26, 2025
-
How Many Tenths Are In A Foot
Jul 26, 2025
-
How Much Is 1 4 Of An Inch
Jul 26, 2025
-
How Many Times Does 15 Go Into 100
Jul 26, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 6 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.