What Is The Lcm Of 8 12 15
Kalali
Jun 13, 2025 · 2 min read
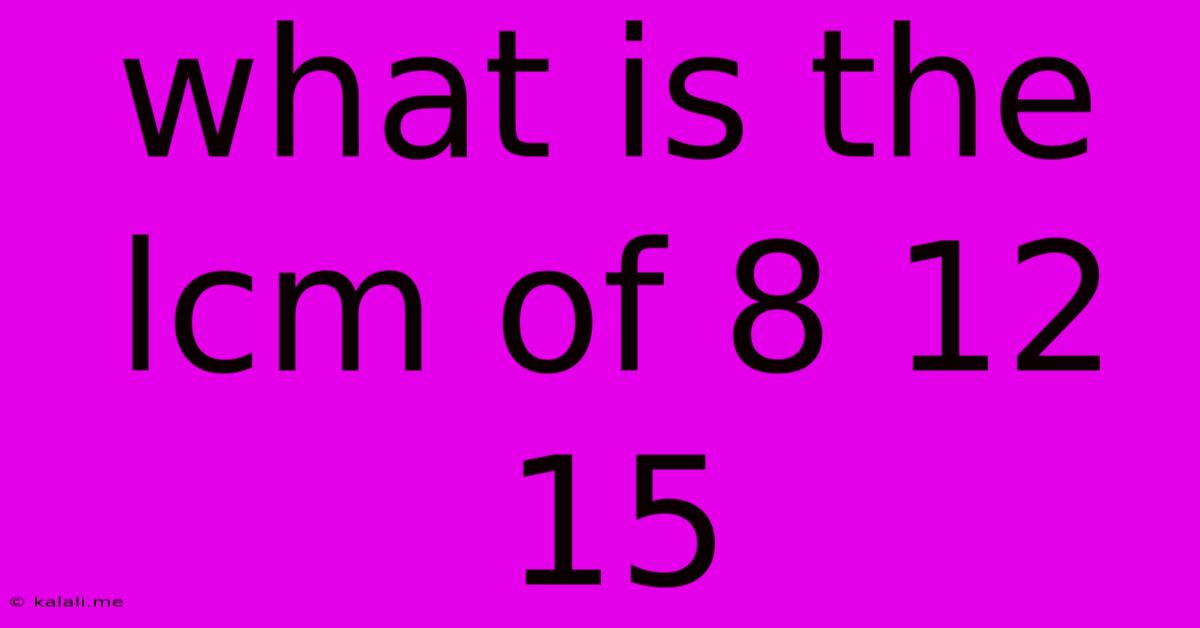
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 12, and 15
This article will guide you through the process of calculating the least common multiple (LCM) of 8, 12, and 15. Understanding LCM is crucial in various mathematical applications, from simplifying fractions to solving problems involving cycles and periodic events. This guide will explain different methods, ensuring you understand the concept thoroughly.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) is the smallest positive integer that is a multiple of two or more numbers. It represents the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Finding the LCM is particularly useful when working with fractions, determining when events will coincide, or solving problems involving cycles.
Methods for Finding the LCM of 8, 12, and 15
There are several ways to calculate the LCM. Let's explore two common methods:
1. Listing Multiples Method
This method involves listing the multiples of each number until you find the smallest common multiple. While simple for smaller numbers, it becomes less efficient with larger numbers.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 60, 72, 80, 96, 120, ...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, ...
By comparing the lists, we can see that the smallest common multiple is 120. Therefore, the LCM of 8, 12, and 15 is 120.
2. Prime Factorization Method
This method is more efficient for larger numbers and involves finding the prime factorization of each number.
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 12 = 2 x 2 x 3 = 2² x 3
- 15 = 3 x 5
-
Identify the highest power of each prime factor:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
- LCM(8, 12, 15) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Therefore, using prime factorization, we again find that the LCM of 8, 12, and 15 is 120.
Conclusion
Both methods demonstrate that the least common multiple of 8, 12, and 15 is 120. The prime factorization method is generally preferred for its efficiency, especially when dealing with larger numbers or a greater number of integers. Understanding how to calculate the LCM is a fundamental skill in mathematics with applications across various fields. Now you're equipped to tackle similar LCM problems with confidence!
Latest Posts
Latest Posts
-
How Many Factors Does 240 Have
Jun 14, 2025
-
Mass Moment Of Inertia For A Circle
Jun 14, 2025
-
What Are All The Factors Of 44
Jun 14, 2025
-
What Is The Difference Between Statute And Common Law
Jun 14, 2025
-
How To Convert Moles Into Grams
Jun 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 12 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.