What Is The Least Common Multiple Of 7 And 9
Kalali
Mar 31, 2025 · 5 min read
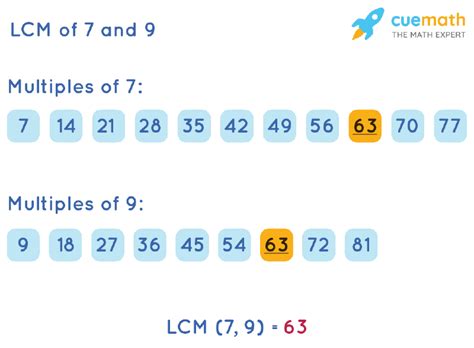
Table of Contents
What is the Least Common Multiple (LCM) of 7 and 9? A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple task, especially for smaller numbers like 7 and 9. However, understanding the underlying principles and exploring different methods for calculating the LCM provides a valuable insight into fundamental number theory concepts. This article will not only answer the question "What is the LCM of 7 and 9?" but also delve deeper into the mathematical concepts involved, exploring various calculation methods and their applications.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a crucial concept in various mathematical fields, including:
- Fraction Arithmetic: Finding the LCM is essential when adding or subtracting fractions with different denominators. You need to find the LCM of the denominators to create a common denominator.
- Modular Arithmetic: LCM plays a key role in solving problems involving congruences and modular arithmetic.
- Scheduling Problems: In real-world scenarios, LCM is used to determine the timing of events that occur periodically, such as the synchronization of machines or the scheduling of recurring tasks.
Key Properties of LCM:
- Commutative Property: The LCM of two numbers is the same regardless of the order; LCM(a, b) = LCM(b, a).
- Associative Property: The LCM of three or more numbers can be calculated by finding the LCM of two numbers at a time; LCM(a, b, c) = LCM(LCM(a, b), c).
- Identity Property: The LCM of any number and 1 is the number itself; LCM(a, 1) = a.
- Relationship with Greatest Common Divisor (GCD): The LCM and GCD of two numbers are related by the formula: LCM(a, b) * GCD(a, b) = a * b. This relationship provides an alternative method for calculating the LCM.
Calculating the LCM of 7 and 9: Different Approaches
There are several ways to find the LCM of 7 and 9. Let's explore the most common methods:
1. Listing Multiples Method
This method is straightforward for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72...
Notice that the smallest multiple common to both lists is 63. Therefore, the LCM(7, 9) = 63.
This method becomes less efficient with larger numbers.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. It's a more efficient and systematic approach, especially for larger numbers.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 9: 3² (9 = 3 x 3)
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 3 is 3² = 9
- The highest power of 7 is 7¹ = 7
Multiply these highest powers together: 9 * 7 = 63. Therefore, LCM(7, 9) = 63.
This method is generally preferred for its efficiency and applicability to larger numbers.
3. Using the GCD (Greatest Common Divisor)
As mentioned earlier, the LCM and GCD are related through the formula: LCM(a, b) * GCD(a, b) = a * b.
First, we need to find the GCD of 7 and 9. Since 7 and 9 have no common factors other than 1, their GCD is 1.
Now, we can use the formula:
LCM(7, 9) * GCD(7, 9) = 7 * 9 LCM(7, 9) * 1 = 63 LCM(7, 9) = 63
This method requires calculating the GCD first, which can be done using the Euclidean algorithm or prime factorization. However, it provides an alternative pathway to the solution.
Why is Understanding LCM Important? Real-world Applications
The concept of LCM extends far beyond textbook exercises. Its practical applications are numerous and impactful across various domains:
1. Scheduling and Synchronization:
Imagine two machines operating on a cycle. One machine completes a task every 7 minutes, and the other every 9 minutes. To determine when both machines will complete a task simultaneously, you need to find the LCM of 7 and 9, which is 63 minutes. This concept applies to various scheduling problems, from industrial processes to transportation logistics.
2. Fraction Operations:
Adding or subtracting fractions requires a common denominator. The LCM of the denominators is the most efficient common denominator. For example, adding 1/7 and 1/9 necessitates finding the LCM of 7 and 9 (63), converting the fractions to 9/63 and 7/63 respectively, then adding them to obtain 16/63.
3. Music Theory:
Musical harmony and rhythm often rely on finding common multiples of frequencies or time intervals. Understanding LCM helps in creating harmonious musical compositions and analyzing rhythmic structures.
4. Computer Science:
In programming and algorithm design, LCM is utilized in tasks such as process synchronization, data structure optimization, and scheduling of concurrent operations.
5. Engineering:
LCM finds applications in various engineering fields, including gear design (ensuring proper meshing of gears with different numbers of teeth), signal processing, and control systems.
Beyond the Basics: Extending LCM Calculations to More Than Two Numbers
The methods described above can be extended to calculate the LCM of more than two numbers. The prime factorization method remains particularly efficient:
Example: Find the LCM of 7, 9, and 10.
-
Prime Factorization:
- 7 = 7
- 9 = 3²
- 10 = 2 * 5
-
Identify Highest Powers: The highest powers of the prime factors are 2¹, 3², 5¹, and 7¹.
-
Calculate LCM: LCM(7, 9, 10) = 2 * 3² * 5 * 7 = 630
Therefore, the least common multiple of 7, 9, and 10 is 630.
The listing multiples method becomes impractical with more numbers, while the GCD method requires iterative application of the GCD calculation. Prime factorization offers the most straightforward approach for calculating the LCM of multiple numbers.
Conclusion: The Power of Simple Concepts in Number Theory
This deep dive into the LCM of 7 and 9 reveals that even seemingly simple mathematical concepts hold significant power and utility. The ability to calculate the LCM is crucial not only for solving mathematical problems but also for addressing real-world challenges across various disciplines. Mastering different calculation methods, especially prime factorization, empowers individuals to tackle more complex problems and appreciate the elegance and practical relevance of fundamental number theory. The seemingly simple answer – 63 – is a gateway to a much broader understanding of mathematical principles and their widespread applications.
Latest Posts
Latest Posts
-
22 5 Out Of 30 As A Percentage
Apr 01, 2025
-
How Do You Write 2 As A Decimal
Apr 01, 2025
-
How Many Inches Are In 1 1 2
Apr 01, 2025
-
What Percent Of 600 Is 3
Apr 01, 2025
-
How Tall Is 24 Inches In Feet
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
