What Is The Least Common Multiple Of 9 And 10
Kalali
Apr 17, 2025 · 5 min read
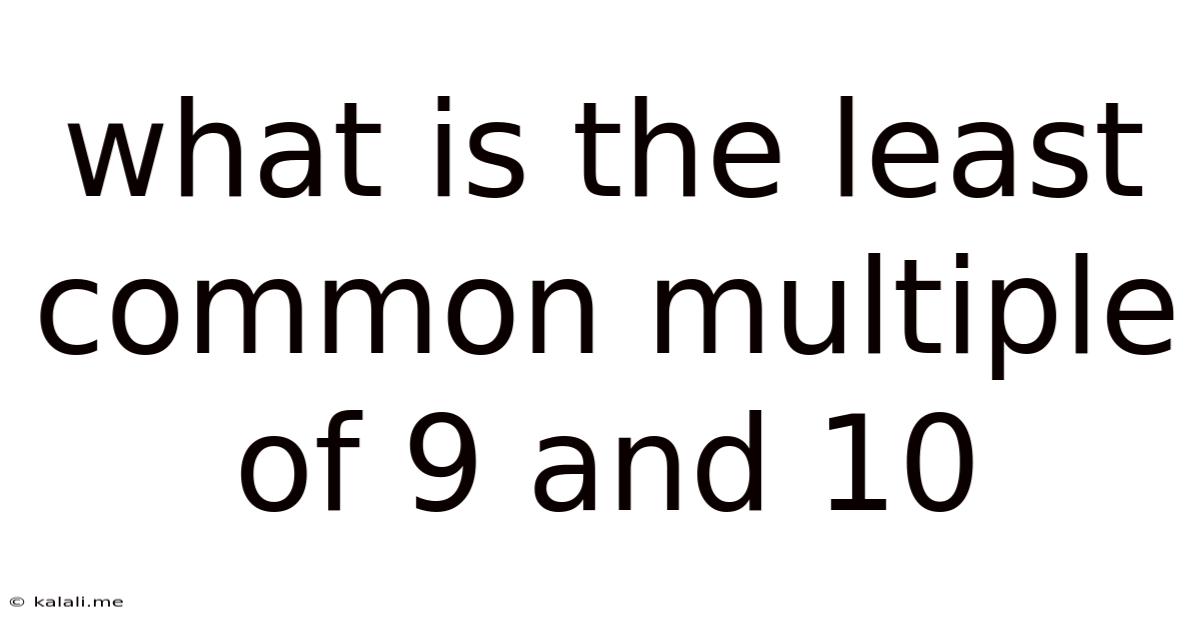
Table of Contents
What is the Least Common Multiple (LCM) of 9 and 10? A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts opens doors to more complex mathematical explorations. This article will delve into determining the LCM of 9 and 10, explaining not only the solution but also the theoretical foundations and practical applications of this fundamental concept in number theory. We'll also explore different methods for calculating the LCM, comparing their efficiency and suitability for various scenarios. This comprehensive guide is designed to provide a thorough understanding of LCM, particularly focusing on the specific example of 9 and 10, for students, educators, and anyone interested in expanding their mathematical knowledge.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. This concept is crucial in various mathematical fields and practical applications, from scheduling tasks to simplifying fractions and solving algebraic equations.
Methods for Calculating LCM
Several methods can be employed to find the LCM of two or more numbers. Let's examine the most common approaches, focusing on their application to find the LCM of 9 and 10:
1. Listing Multiples Method
This is the most intuitive approach, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
By comparing the lists, we see that the smallest common multiple is 90. Therefore, the LCM(9, 10) = 90. This method is straightforward but can become cumbersome for larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present in the factorizations.
- Prime factorization of 9: 3²
- Prime factorization of 10: 2 × 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2¹
- Highest power of 3: 3²
- Highest power of 5: 5¹
Multiplying these together: 2¹ × 3² × 5¹ = 2 × 9 × 5 = 90. Therefore, the LCM(9, 10) = 90. This method is generally preferred for its efficiency and systematic approach.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship provides another method for calculating the LCM.
First, we find the GCD of 9 and 10 using the Euclidean algorithm or prime factorization.
- Prime factorization of 9: 3²
- Prime factorization of 10: 2 × 5
The GCD is 1 (as there are no common prime factors).
Now, using the relationship: LCM(a, b) = (a × b) / GCD(a, b)
LCM(9, 10) = (9 × 10) / 1 = 90. This method is particularly useful when dealing with larger numbers where finding the GCD is easier than directly finding the LCM.
Why 90? A Deeper Look
The LCM of 9 and 10 being 90 isn't just a result of calculation; it reflects the underlying structure of these numbers. 90 is the smallest number that contains all the prime factors of both 9 and 10, each raised to its highest power. This highlights the fundamental connection between prime factorization and the concept of LCM. Understanding this connection allows us to predict and explain the results more meaningfully than simply applying a formula. This is key to understanding more complex number theory concepts.
Applications of LCM
The LCM finds applications in numerous areas:
-
Scheduling: Determining when events will occur simultaneously. For example, if one event repeats every 9 days and another every 10 days, the LCM (90) indicates they will coincide every 90 days.
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is the LCM of the denominators.
-
Modular Arithmetic: Solving congruences and other problems in modular arithmetic often involves finding the LCM.
-
Music Theory: Understanding rhythmic patterns and musical intervals involves concepts related to LCM.
-
Computer Science: Various algorithms and data structures utilize LCM concepts, particularly in areas of scheduling and resource management.
Beyond the Basics: Extending the Concept
The concept of LCM extends beyond two numbers. We can find the LCM of any number of integers using the same principles. For example, finding the LCM of 3, 4, and 6 involves finding the prime factorization of each number and then selecting the highest power of each prime factor present.
The prime factorization method remains the most efficient and versatile method for finding the LCM of multiple numbers. This method allows for a systematic approach that scales well to larger numbers and a greater number of inputs, unlike the listing method which quickly becomes impractical.
Conclusion: The Importance of Understanding LCM
Determining the least common multiple of 9 and 10, while seemingly a simple arithmetic problem, serves as a gateway to understanding more profound concepts in number theory. The various methods for calculating the LCM – listing multiples, prime factorization, and using the GCD – highlight different approaches to solving mathematical problems, each with its strengths and weaknesses. Understanding the theoretical underpinnings of LCM, coupled with the ability to apply various calculation methods, empowers us to tackle more complex mathematical challenges and appreciate the elegance and interconnectedness of mathematical principles. The practical applications of LCM across various fields reinforce its importance as a fundamental concept in mathematics and beyond. The fact that the LCM of 9 and 10 is 90 is not merely a numerical result but a manifestation of the underlying structure and relationships between these numbers, showcasing the beauty and power of number theory.
Latest Posts
Latest Posts
-
24 Oz Is How Many Milliliters
Apr 19, 2025
-
How Many Protons Are In F
Apr 19, 2025
-
How Many Inches Is 2 2 Cm
Apr 19, 2025
-
How Much Feet Is 44 Inches
Apr 19, 2025
-
What Is An 8 Out Of 12
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 9 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.