What Is The Least Common Multiple Of 9 And 15
Kalali
Apr 04, 2025 · 5 min read
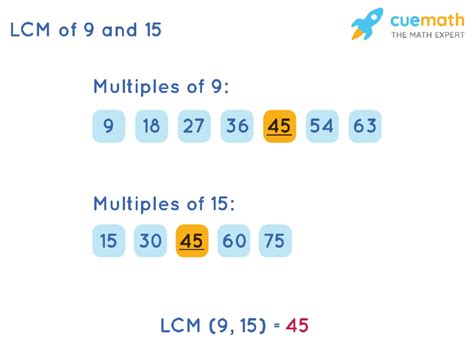
Table of Contents
What is the Least Common Multiple (LCM) of 9 and 15? A Deep Dive into Finding LCMs
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to scheduling events. This article will delve deep into determining the LCM of 9 and 15, exploring multiple methods and illustrating the broader principles behind LCM calculations. We'll also touch upon the importance of LCMs in various real-world scenarios.
Understanding Least Common Multiples (LCMs)
Before we tackle the specific problem of finding the LCM of 9 and 15, let's establish a firm grasp of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) of your numbers can divide into evenly.
Key Concepts:
- Multiple: A multiple of a number is the result of multiplying that number by any integer (e.g., multiples of 3 are 3, 6, 9, 12, 15...).
- Common Multiple: A common multiple of two or more numbers is a number that is a multiple of all of them. For example, common multiples of 2 and 3 include 6, 12, 18, 24...
- Least Common Multiple (LCM): The smallest of the common multiples.
Methods for Finding the LCM of 9 and 15
Several methods can be employed to find the LCM of 9 and 15. We'll explore three common approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We simply list the multiples of each number until we find the smallest multiple they share.
Multiples of 9: 9, 18, 27, 36, 45, 54, 63... Multiples of 15: 15, 30, 45, 60, 75...
As we can see, the smallest number that appears in both lists is 45. Therefore, the LCM of 9 and 15 is 45.
This method is effective for small numbers but becomes cumbersome and time-consuming for larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
Prime Factorization of 9: 3 x 3 = 3² Prime Factorization of 15: 3 x 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
Therefore, the LCM of 9 and 15 is 3² x 5 = 9 x 5 = 45.
This method is more systematic and scalable, making it suitable for larger numbers where listing multiples would be impractical.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers evenly. The formula connecting LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 9 and 15 using the Euclidean algorithm:
- Divide the larger number (15) by the smaller number (9): 15 ÷ 9 = 1 with a remainder of 6.
- Replace the larger number with the smaller number (9) and the smaller number with the remainder (6): 9 ÷ 6 = 1 with a remainder of 3.
- Repeat: 6 ÷ 3 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 3.
Now, we can use the formula:
LCM(9, 15) x GCD(9, 15) = 9 x 15 LCM(9, 15) x 3 = 135 LCM(9, 15) = 135 ÷ 3 = 45
This method demonstrates the interconnectedness between LCM and GCD, providing an alternative approach to finding the LCM.
Real-World Applications of LCM
The concept of LCM extends far beyond the realm of abstract mathematics. It finds practical applications in numerous real-world scenarios:
1. Scheduling and Timing
Imagine you have two machines that operate on different cycles. One machine completes a cycle every 9 minutes, and another every 15 minutes. To determine when both machines will complete a cycle simultaneously, you need to find the LCM of 9 and 15, which is 45 minutes. This is the shortest time interval when both machines will be at the starting point of their cycle simultaneously. This principle applies to various scheduling problems, such as coordinating bus schedules, factory production lines, or even planning events.
2. Fraction Arithmetic
LCMs are essential when adding or subtracting fractions with different denominators. To add fractions like 1/9 and 1/15, you need to find a common denominator, which is the LCM of 9 and 15 (45). This allows you to express the fractions with the same denominator before performing addition or subtraction.
3. Gear Ratios and Mechanical Systems
In mechanical engineering, LCMs play a crucial role in designing gear ratios and other mechanical systems. Understanding the LCM helps engineers ensure that different components of a machine operate harmoniously and efficiently.
4. Music Theory
Musical intervals and harmonies are often expressed using ratios of frequencies. Finding common multiples and least common multiples helps musicians and composers understand the relationships between different notes and chords.
5. Project Management
In project management, LCM can help synchronize tasks with varying durations. Determining when multiple projects with differing completion timelines align is crucial for resource allocation and efficient workflow.
Conclusion: The Power of LCM
The LCM, seemingly a simple mathematical concept, holds significant power and practical relevance. Whether you're simplifying fractions, scheduling tasks, or designing complex mechanical systems, understanding how to find the LCM is a valuable skill. This article has demonstrated multiple methods for calculating the LCM, highlighting their strengths and weaknesses, and providing a deeper understanding of its applications in the real world. Remember, the choice of method depends on the context and complexity of the numbers involved. For smaller numbers, listing multiples might suffice, but for larger numbers, prime factorization or the GCD method are more efficient and practical. Mastering the LCM is key to solving a wide range of mathematical and real-world problems.
Latest Posts
Latest Posts
-
How Much Is 45 Degrees Celsius In Fahrenheit
Apr 04, 2025
-
What Is 34 Inches In Feet
Apr 04, 2025
-
Cuanto Es 25 Grados Fahrenheit En Centigrados
Apr 04, 2025
-
Do Diagonals Of A Parallelogram Intersect At Right Angles
Apr 04, 2025
-
Why Would Dark Moths Have An Advantage
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 9 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
