What Is The Percent Of 1/6
Kalali
Apr 20, 2025 · 5 min read
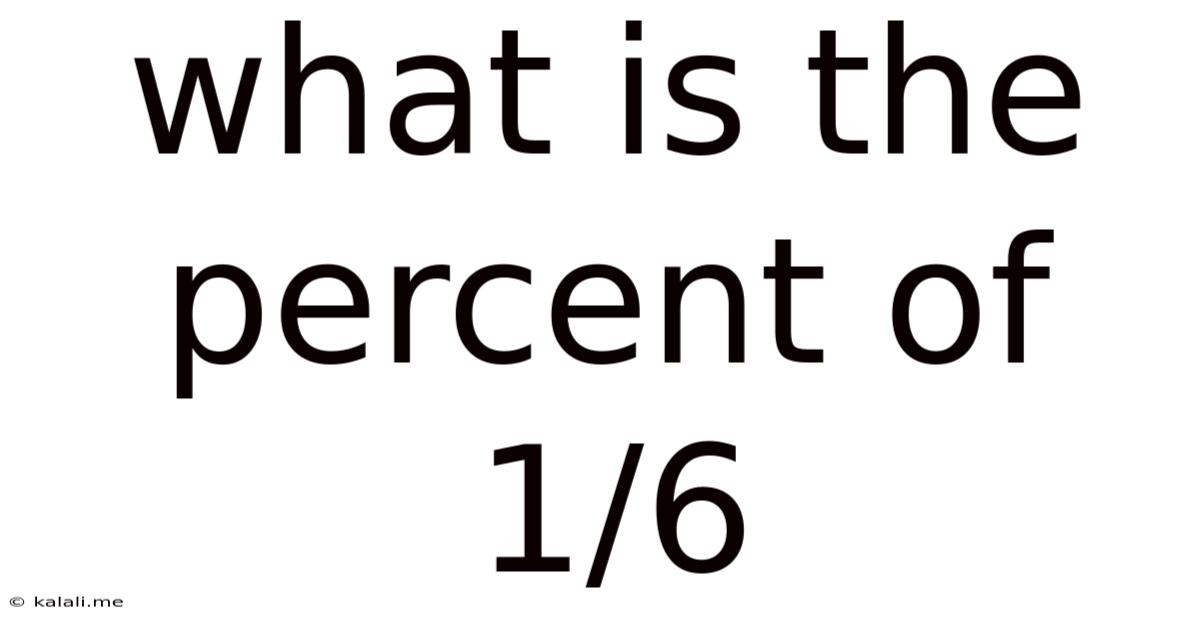
Table of Contents
What is the Percent of 1/6? A Deep Dive into Fractions, Decimals, and Percentages
What is the percentage equivalent of 1/6? This seemingly simple question opens the door to a broader understanding of mathematical concepts fundamental to everyday life, from calculating discounts to understanding financial reports. This article will not only answer that core question but also delve into the methods behind the calculation, exploring the relationship between fractions, decimals, and percentages, and offering practical applications to solidify your understanding. Understanding these conversions is crucial for various fields, from finance and data analysis to cooking and construction.
Meta Description: This comprehensive guide explains how to convert the fraction 1/6 into a percentage, detailing the steps involved and providing practical examples. Learn about the interconnectedness of fractions, decimals, and percentages and how to confidently perform these conversions.
Understanding the Building Blocks: Fractions, Decimals, and Percentages
Before diving into the specific calculation, let's establish a solid foundation by understanding the core concepts:
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many parts make up the whole. 1/6 means you have one part out of a total of six equal parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with the decimal point separating the whole number from the fractional part. For example, 0.5 represents one-half (1/2).
-
Percentages: Percentages express a number as a fraction of 100. The symbol "%" represents "per hundred." 50%, for example, means 50 out of 100, which is equivalent to 1/2 or 0.5.
These three representational systems are interchangeable, allowing for flexibility in mathematical operations and problem-solving. Understanding their relationships is key to mastering mathematical conversions.
Calculating the Percentage Equivalent of 1/6: Method 1 - Division
The most straightforward method to convert a fraction to a percentage is through division. Follow these steps:
-
Divide the numerator by the denominator: In the fraction 1/6, divide 1 by 6. This gives you 0.166666... This is a recurring decimal, meaning the '6' repeats infinitely.
-
Multiply the decimal by 100: To convert the decimal to a percentage, multiply the result from step 1 by 100. 0.166666... x 100 = 16.6666...%
-
Round to the desired precision: Since the decimal is recurring, you'll need to round the percentage to a certain number of decimal places. Commonly, this is rounded to two decimal places, resulting in 16.67%.
Therefore, 1/6 is approximately equal to 16.67%.
Calculating the Percentage Equivalent of 1/6: Method 2 - Proportion
Another approach uses the concept of proportions. We know that a percentage is a fraction out of 100. We can set up a proportion to solve for the unknown percentage:
1/6 = x/100
To solve for 'x', cross-multiply:
6x = 100
x = 100/6
x ≈ 16.67
Therefore, x = 16.67%
This method reinforces the understanding that percentages are simply fractions with a denominator of 100.
Practical Applications of Converting Fractions to Percentages
The ability to convert fractions to percentages is invaluable in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, and profit margins often involves converting fractions to percentages. For instance, understanding that a 1/6 discount represents a 16.67% reduction helps in making informed purchasing decisions.
-
Data Analysis: Representing data as percentages provides a clear and concise way to compare different proportions. For example, if 1/6 of a survey sample responded positively to a particular question, this can be easily communicated as a 16.67% positive response rate.
-
Cooking and Baking: Recipes often use fractions to represent ingredient quantities. Converting these fractions to percentages can aid in scaling recipes up or down.
-
Construction and Engineering: Precise measurements and proportions are crucial in construction. Converting fractions to percentages aids in ensuring accuracy and consistency.
-
Everyday Life: Understanding percentages improves your ability to interpret and analyze data in various contexts, from understanding sales tax to comparing product prices.
Understanding Recurring Decimals and Rounding
The conversion of 1/6 to a percentage results in a recurring decimal (0.16666...). Dealing with recurring decimals requires understanding rounding:
-
Rounding: The process of approximating a number to a specified number of decimal places. If the digit after the desired place is 5 or greater, you round up; otherwise, you round down.
-
Significant Figures: The number of digits in a value that contribute to its precision. Rounding to a specific number of significant figures maintains accuracy while simplifying the representation.
In the case of 1/6, rounding to two decimal places gives us 16.67%. However, it's important to remember that this is an approximation; the true value is 16.6666...% The level of precision required depends on the context of the application.
Beyond 1/6: Mastering Fraction-to-Percentage Conversions
The principles discussed for converting 1/6 can be applied to any fraction. The general process remains the same: divide the numerator by the denominator and multiply the result by 100. Practice with various fractions will solidify your understanding and build confidence in performing these conversions. Consider working through examples like 1/3, 2/5, and 3/8 to reinforce your skills.
Advanced Considerations: Working with Complex Fractions and Percentages
While 1/6 is a relatively simple fraction, you might encounter more complex scenarios:
-
Improper Fractions: Fractions where the numerator is larger than the denominator (e.g., 7/4). These can be converted to mixed numbers (1 ¾) before converting to a percentage or directly converted to a decimal first then to a percentage.
-
Complex Fractions: Fractions with fractions in the numerator or denominator (e.g., (1/2)/(1/3)). These require careful simplification before converting to a percentage.
-
Percentage Increase/Decrease: These calculations build upon the foundation of converting fractions to percentages. They involve determining the percentage change between two values.
Mastering these advanced concepts requires a solid grasp of fundamental fractional arithmetic.
Conclusion: The Power of Percentage Conversions
Understanding how to convert fractions to percentages empowers you to navigate a wide range of mathematical problems. The seemingly simple task of converting 1/6 to a percentage unlocks a world of applications in finance, data analysis, and everyday life. By mastering this fundamental conversion, you equip yourself with a valuable skill applicable to numerous contexts. Remember to practice regularly, explore different methods, and apply your knowledge to real-world scenarios to fully grasp the power of percentage conversions.
Latest Posts
Latest Posts
-
What Are Holes In A Graph
Apr 22, 2025
-
600 Ml Is How Many Cups
Apr 22, 2025
-
How Many Hours Is 119 Minutes
Apr 22, 2025
-
Waves Interact With And Other
Apr 22, 2025
-
154 Cm Is How Many Feet
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 1/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.