What Is The Percent Of 17/20
Kalali
Apr 14, 2025 · 5 min read
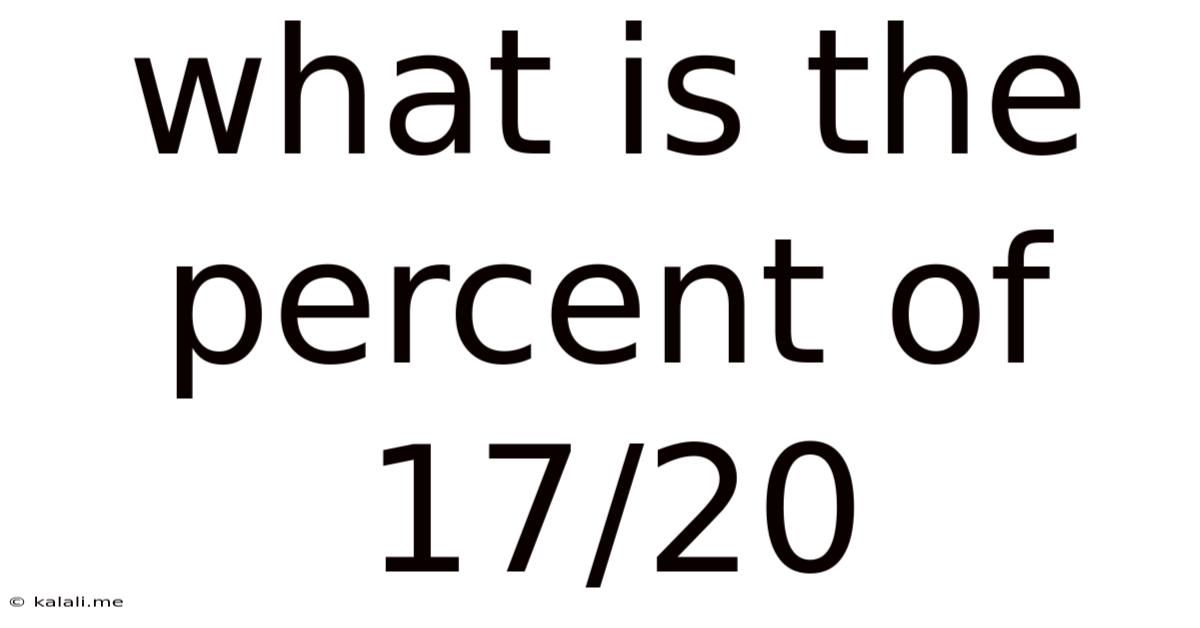
Table of Contents
What is the Percentage of 17/20? A Deep Dive into Fractions, Decimals, and Percentages
What is 17/20 as a percentage? This seemingly simple question opens the door to a broader understanding of fundamental mathematical concepts, crucial for everyday life and various academic and professional pursuits. This article will not only answer the question directly but will also explore the underlying principles of converting fractions to percentages, providing you with the tools to tackle similar calculations with confidence. We'll delve into practical applications and explore related concepts to solidify your understanding.
Understanding the Core Concepts: Fractions, Decimals, and Percentages
Before we calculate the percentage equivalent of 17/20, let's clarify the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our example, 17/20, 17 is the numerator and 20 is the denominator. It means 17 out of 20 parts.
-
Decimals: A decimal is a way of expressing a fraction using base-10. The decimal point separates the whole number from the fractional part. For instance, 0.5 is equivalent to ½, and 0.75 is equivalent to ¾.
-
Percentages: A percentage represents a fraction or decimal as a proportion of 100. The symbol "%" signifies "per hundred." For example, 50% means 50 out of 100, or ½.
Calculating 17/20 as a Percentage: The Step-by-Step Process
There are two primary methods to convert 17/20 into a percentage:
Method 1: Converting the Fraction to a Decimal, then to a Percentage
-
Divide the numerator by the denominator: Divide 17 by 20. This gives you 0.85.
-
Multiply the decimal by 100: Multiply 0.85 by 100. This gives you 85.
-
Add the percentage symbol: Add the "%" symbol to indicate that the result is a percentage.
Therefore, 17/20 is equal to 85%.
Method 2: Direct Conversion Using Proportions
This method uses the concept of proportion. We know that a percentage is a fraction out of 100. We can set up a proportion:
17/20 = x/100
To solve for 'x' (the percentage), we cross-multiply:
20x = 1700
x = 1700 / 20
x = 85
Therefore, 17/20 is equal to 85%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various aspects of life:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely on percentage calculations. For example, understanding that a 10% discount on a $100 item saves you $10 is a direct application of percentage calculation.
-
Academics: Percentages are extensively used to represent grades, test scores, and progress in various subjects. A student scoring 85% on a test indicates they answered 85 out of 100 questions correctly.
-
Statistics: Percentages are essential for analyzing data, representing proportions, and communicating findings. For instance, stating that 70% of survey respondents prefer a certain product provides valuable statistical insight.
-
Everyday Life: Calculating tips in restaurants, understanding sale prices, determining the percentage of ingredients in recipes, and even interpreting weather forecasts (e.g., an 80% chance of rain) all involve percentage calculations.
Expanding on the Concept: Working with Different Fractions
The methods described above can be applied to convert any fraction into a percentage. Let's explore a few examples:
-
Converting 3/4 to a percentage:
- 3 ÷ 4 = 0.75
- 0.75 x 100 = 75
- Therefore, 3/4 = 75%
-
Converting 1/5 to a percentage:
- 1 ÷ 5 = 0.2
- 0.2 x 100 = 20
- Therefore, 1/5 = 20%
-
Converting 7/8 to a percentage:
- 7 ÷ 8 = 0.875
- 0.875 x 100 = 87.5
- Therefore, 7/8 = 87.5%
Dealing with Improper Fractions and Mixed Numbers
An improper fraction is a fraction where the numerator is larger than the denominator (e.g., 22/10). A mixed number combines a whole number and a fraction (e.g., 2 1/2).
To convert an improper fraction to a percentage, first, convert it into a mixed number or a decimal, then follow the steps outlined previously. For example, 22/10 can be simplified to 2 2/10 or 2.2. Then:
- 2.2 x 100 = 220%
To convert a mixed number to a percentage, first convert it into an improper fraction, then follow the steps:
- 2 1/2 = 5/2
- 5 ÷ 2 = 2.5
- 2.5 x 100 = 250%
Advanced Applications and Related Concepts
The ability to convert fractions to percentages is a fundamental skill that lays the groundwork for understanding more complex mathematical concepts:
-
Ratio and Proportion: Percentages are a direct application of ratios and proportions. Understanding these concepts is vital for solving problems involving scaling, scaling recipes, or determining relative sizes.
-
Probability: Percentages are frequently used to express probabilities. For example, a 25% chance of winning a game means that there is a one in four probability of success.
-
Data Analysis and Interpretation: Percentages play a crucial role in summarizing and interpreting data. They help us understand trends, make comparisons, and draw meaningful conclusions.
Conclusion: Mastering Percentage Calculations for Success
The ability to convert fractions, such as 17/20, to percentages is a valuable skill with widespread applications. Understanding the underlying principles—the relationship between fractions, decimals, and percentages—empowers you to tackle various mathematical challenges confidently. By mastering these concepts, you not only improve your mathematical proficiency but also enhance your ability to analyze data, solve problems, and interpret information in various aspects of your life. Remember the two key methods outlined above, and practice with different fractions to solidify your understanding and build your skills. The more you practice, the easier and more intuitive these calculations will become.
Latest Posts
Latest Posts
-
What Is 9 5 Inches In Cm
Apr 15, 2025
-
How Much Is 155 Cm In Feet
Apr 15, 2025
-
What Is The Percentage Of 0 5
Apr 15, 2025
-
What Is 24 Inches In Cm
Apr 15, 2025
-
How Many Cups Are In 24 Oz Of Water
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 17/20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.