What Is The Percent Of 2/25
Kalali
Apr 09, 2025 · 5 min read
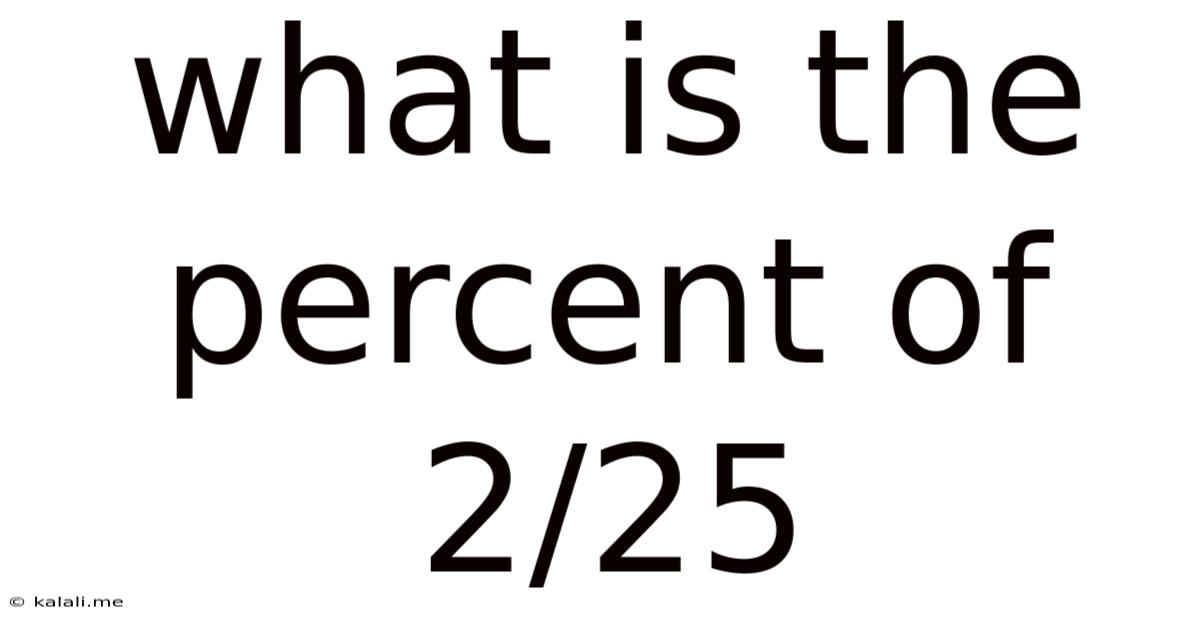
Table of Contents
What is the Percentage of 2/25? A Deep Dive into Fractions, Decimals, and Percentages
This article explores the seemingly simple question: what is the percentage of 2/25? While the answer might seem immediately obvious to some, we'll delve deeper than a simple calculation. We'll unpack the underlying concepts of fractions, decimals, and percentages, exploring their interrelationships and providing a comprehensive understanding of how to convert between them. This will equip you with the skills to tackle similar percentage problems with confidence and even help you understand more complex scenarios involving percentages.
Meta Description: Learn how to calculate the percentage equivalent of 2/25. This comprehensive guide explains the conversion process from fractions to decimals to percentages, offering valuable insights into fundamental mathematical concepts and practical applications.
Understanding Fractions
Before we tackle the percentage, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). In the fraction 2/25, 2 is the numerator and 25 is the denominator. This means we are considering 2 parts out of a total of 25 parts.
Fractions can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. In this case, the GCD of 2 and 25 is 1, meaning the fraction 2/25 is already in its simplest form. This is important because simplified fractions often make calculations easier.
Converting Fractions to Decimals
To convert a fraction to a decimal, we simply divide the numerator by the denominator. For 2/25, we perform the division: 2 ÷ 25 = 0.08. This means that 2/25 is equivalent to 0.08 as a decimal. This decimal representation is crucial for the next step – converting to a percentage.
Understanding decimal places is key. The first digit after the decimal point represents tenths (1/10), the second represents hundredths (1/100), and so on. In 0.08, the 8 is in the hundredths place, meaning it represents 8/100.
Converting Decimals to Percentages
The conversion from decimals to percentages is straightforward. A percentage is simply a fraction expressed as a number out of 100. To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent sign (%).
In our example, 0.08 multiplied by 100 is 8. Therefore, 0.08 is equivalent to 8%. So, the answer to our original question – what is the percentage of 2/25? – is 8%.
Alternative Method: Direct Conversion from Fraction to Percentage
We can also convert a fraction directly to a percentage without going through the decimal stage. This involves multiplying the fraction by 100%. For 2/25, this looks like:
(2/25) * 100% = (2 * 100) / 25 % = 200 / 25 % = 8%
This method provides a more direct route to the answer, highlighting the relationship between fractions and percentages.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is a fundamental skill applicable across numerous real-world situations:
-
Financial calculations: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely on percentage calculations. For example, a 10% discount on a $100 item means a savings of $10.
-
Data analysis: Percentages are frequently used to represent proportions and trends in data. In surveys and statistical reports, percentages help visualize and understand the distribution of responses or the prevalence of certain characteristics. For instance, if 8% of survey respondents prefer a particular product, this provides valuable market research information.
-
Scientific calculations: Percentage change is frequently used to express differences between two values, such as growth rates in populations or changes in chemical concentrations.
-
Everyday life: Calculating tips in restaurants, determining sale prices, or understanding nutritional information on food labels all involve using percentages.
Expanding on the Concept: Working with More Complex Fractions
While 2/25 was a relatively simple fraction, let's consider how to handle more complex scenarios. For instance, what if the fraction was 7/12? The process remains the same:
- Conversion to Decimal: 7 ÷ 12 ≈ 0.5833 (we'll round to four decimal places for accuracy)
- Conversion to Percentage: 0.5833 * 100% ≈ 58.33%
Or, using the direct method:
(7/12) * 100% ≈ 58.33%
This demonstrates the adaptability of these conversion methods. Even with more complicated fractions, the fundamental principles remain consistent.
Dealing with Recurring Decimals
Some fractions, when converted to decimals, result in recurring decimals (decimals that repeat infinitely). For example, 1/3 converts to 0.3333... When converting these to percentages, we typically round to a reasonable number of decimal places for practical purposes. For instance, 1/3 would be approximately 33.33%. The level of rounding depends on the context and the required level of accuracy.
Percentage Increase and Decrease
Beyond simple conversion, understanding percentage increase and decrease is also vital. Suppose a price increases by 15%. To calculate the new price, we add 15% of the original price to the original price. Similarly, for a percentage decrease, we subtract the percentage from the original value. These calculations are widely used in finance, economics, and various other fields.
Error Analysis and Precision
It's crucial to be aware of potential errors introduced by rounding. Rounding off during the conversion process can lead to slight inaccuracies in the final result. The level of precision required depends heavily on the application. In financial calculations, for example, high precision is usually crucial, while in some everyday scenarios, a rough approximation might suffice.
Conclusion: Mastering Percentage Calculations
This in-depth exploration of converting 2/25 to a percentage has served as a springboard to understanding the broader context of fractions, decimals, and percentages. Mastering these conversions is essential not only for solving mathematical problems but also for navigating various aspects of daily life, particularly those involving finance, data analysis, and many other fields. By understanding the underlying principles and methods outlined here, you're well-equipped to confidently tackle a wide range of percentage-related calculations and applications. Remember to always consider the context and required level of precision when working with percentages and rounding decimals. With practice and a clear understanding of the concepts, you will confidently handle any percentage calculation you encounter.
Latest Posts
Latest Posts
-
11 5 Oz Is How Many Cups
Apr 17, 2025
-
How Much Is 55 Inches In Cm
Apr 17, 2025
-
What Is The Least Common Multiple Of 4 And 12
Apr 17, 2025
-
4 Liters Equals How Many Gallons
Apr 17, 2025
-
What Is 3 10 In A Decimal
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 2/25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.