What Is The Percent Of 3/7
Kalali
Apr 25, 2025 · 5 min read
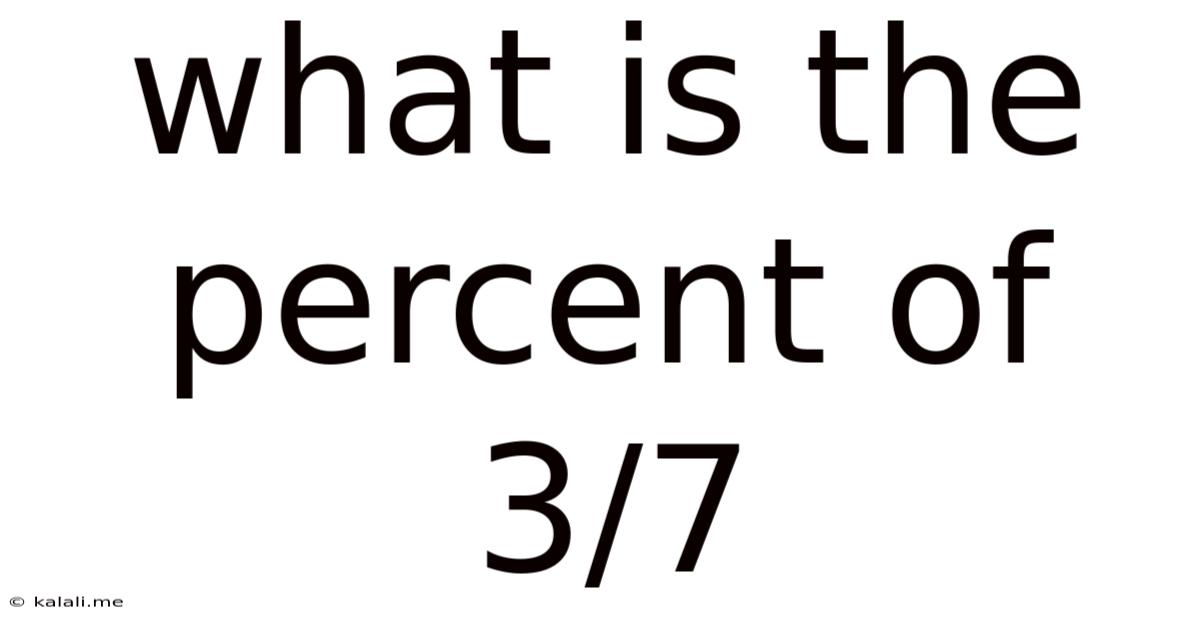
Table of Contents
What is the Percentage of 3/7? A Deep Dive into Fractions, Decimals, and Percentages
What is the percentage of 3/7? This seemingly simple question opens the door to a broader understanding of fundamental mathematical concepts: fractions, decimals, and percentages, and how they interconnect. This article will not only answer the question directly but will also explore the underlying principles, provide multiple methods for solving similar problems, and delve into practical applications. Understanding these concepts is crucial for various aspects of life, from everyday budgeting and shopping to more complex calculations in fields like finance and engineering.
Understanding Fractions, Decimals, and Percentages
Before we tackle the specific problem of converting 3/7 into a percentage, let's solidify our understanding of these core mathematical components:
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 3/7, 3 is the numerator and 7 is the denominator. This means we have 3 parts out of a total of 7 equal parts.
-
Decimals: A decimal is a way of representing a number using a base-ten system. It uses a decimal point to separate the whole number part from the fractional part. For example, 0.5 represents one-half (1/2), and 0.75 represents three-quarters (3/4).
-
Percentages: A percentage is a way of expressing a number as a fraction of 100. It's often denoted by the symbol "%". For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are widely used to represent proportions, rates, and changes.
Calculating the Percentage of 3/7: Method 1 - Direct Conversion
The most straightforward method to determine the percentage of 3/7 involves converting the fraction into a decimal and then multiplying by 100.
-
Divide the numerator by the denominator: 3 ÷ 7 ≈ 0.42857
-
Multiply the decimal by 100: 0.42857 × 100 = 42.857
Therefore, 3/7 is approximately 42.86%. We round to two decimal places for practical purposes.
Calculating the Percentage of 3/7: Method 2 - Using Proportions
This method utilizes the concept of proportions to solve for the unknown percentage. We set up a proportion where the fraction 3/7 is equal to x/100, where 'x' represents the percentage we're trying to find.
-
Set up the proportion: 3/7 = x/100
-
Cross-multiply: 7x = 300
-
Solve for x: x = 300/7 ≈ 42.857
-
Convert to percentage: x ≈ 42.86%
This method reinforces the relationship between fractions and percentages, clearly demonstrating that a percentage is simply a fraction expressed as parts of 100.
Calculating the Percentage of 3/7: Method 3 - Long Division and Conversion
This method emphasizes the process of long division for those who prefer a more manual approach.
-
Perform Long Division: Divide 3 by 7 using long division. This will yield a decimal value. You'll find that the division results in a repeating decimal (0.428571428571...).
-
Multiply by 100: Once you have the decimal approximation (e.g., 0.42857), multiply it by 100 to obtain the percentage.
-
Round to desired precision: Round the result to the nearest hundredth, tenth, or whole number, depending on the level of accuracy required.
Understanding the Repeating Decimal
Notice that the decimal representation of 3/7 (0.428571428571…) is a repeating decimal. This means the sequence of digits "428571" repeats infinitely. This is common when converting fractions with denominators that are not factors of powers of 10 (10, 100, 1000, etc.). When expressing this as a percentage, rounding is necessary for practical application.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages is essential in various real-world scenarios:
-
Discounts and Sales: Determining the discount amount on sale items often involves converting a fractional discount (e.g., 1/3 off) into a percentage.
-
Taxes and Tips: Calculating sales tax or service tips based on a percentage of the total cost requires a clear understanding of percentage conversions.
-
Financial Calculations: Interest rates, loan payments, and investment returns are frequently expressed as percentages.
-
Statistics and Data Analysis: Percentages are widely used to represent proportions and trends in data sets.
-
Scientific Measurements and Experiments: Percentages are frequently used to express error margins, concentrations, and yields in scientific research.
Beyond 3/7: Mastering Fraction-to-Percentage Conversions
The techniques described above can be applied to convert any fraction into a percentage. The key steps remain consistent:
-
Convert the fraction to a decimal: Divide the numerator by the denominator.
-
Multiply the decimal by 100: This converts the decimal to a percentage.
-
Round as needed: Round the percentage to the desired level of accuracy.
Conclusion: The Power of Understanding Fractions, Decimals, and Percentages
This article comprehensively explored the conversion of 3/7 to a percentage, highlighting multiple methods to achieve this. Beyond the specific answer (approximately 42.86%), the focus was on understanding the fundamental relationships between fractions, decimals, and percentages. Mastering these concepts is crucial for navigating various aspects of life, both personal and professional, where quantitative reasoning plays a significant role. The ability to perform these conversions effortlessly empowers you to tackle more complex mathematical problems and confidently interpret data presented in various formats. Remember to practice these methods with different fractions to solidify your understanding and build your mathematical fluency.
Latest Posts
Latest Posts
-
10 Oz Of Water Is How Many Cups
Apr 25, 2025
-
Angle Elevation And Depression Word Problems
Apr 25, 2025
-
How Many Ounces Are In 200 Grams
Apr 25, 2025
-
At Room Temperature Most Metals Are
Apr 25, 2025
-
How Much Is 200 Ml Water In Cups
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 3/7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.