What Is The Percent Of 5/12
Kalali
Apr 11, 2025 · 5 min read
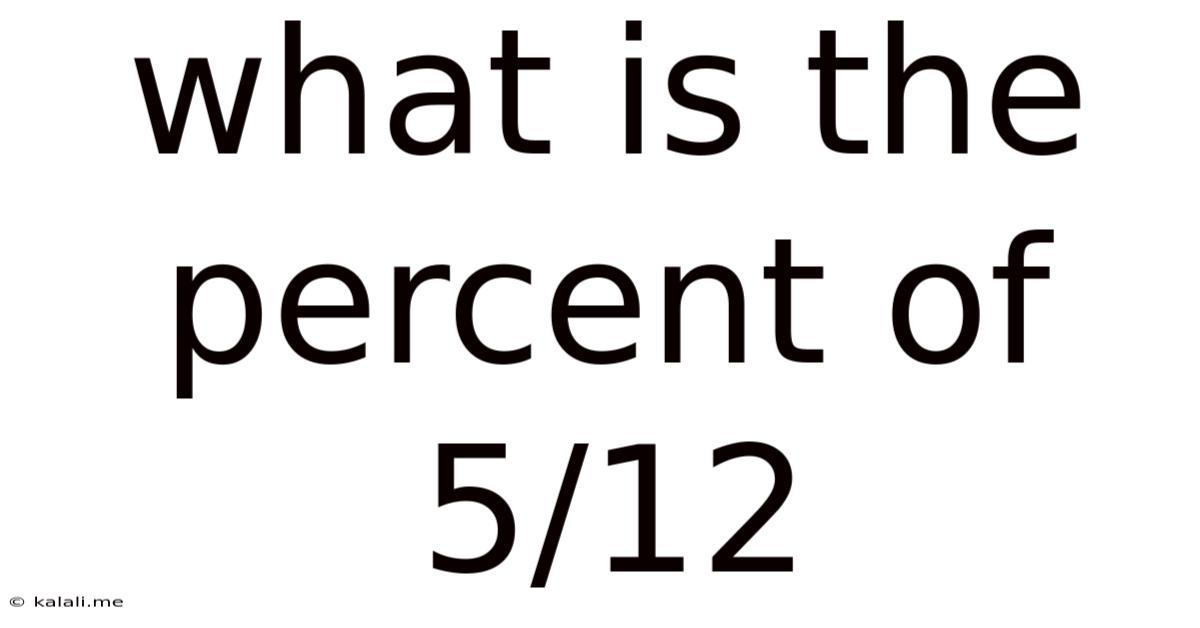
Table of Contents
What is the Percentage of 5/12? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday life. This article will delve deep into the process of converting the fraction 5/12 into a percentage, explaining the method in detail and providing practical examples and extensions to help you master this crucial concept. We'll explore different approaches, address potential pitfalls, and offer tips for applying this knowledge to more complex scenarios.
What is a Percentage?
Before we tackle the conversion, let's clarify the concept of a percentage. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting Fractions to Percentages: The Core Method
The most straightforward method for converting a fraction to a percentage involves two simple steps:
- Convert the fraction to a decimal: Divide the numerator (the top number) by the denominator (the bottom number).
- Multiply the decimal by 100: This will give you the percentage equivalent.
Let's apply this to our fraction, 5/12:
-
Decimal Conversion: 5 ÷ 12 = 0.416666... (the 6 repeats infinitely)
-
Percentage Conversion: 0.416666... × 100 = 41.6666...%
This means that 5/12 is approximately 41.67%. The repeating decimal highlights the importance of understanding rounding and significant figures, which we'll explore further below.
Understanding Rounding and Significant Figures
The repeating decimal in our result (0.416666...) presents a practical challenge. We can't write an infinite number of digits. Therefore, rounding is necessary. The level of precision required depends on the context. Commonly used levels of precision are:
- Nearest whole number: 42% (simple and suitable for estimations)
- One decimal place: 41.7% (offers a bit more accuracy)
- Two decimal places: 41.67% (provides greater accuracy, commonly used in financial calculations)
The choice of rounding significantly impacts the accuracy of the result. Always consider the context to determine the appropriate level of precision. Using too many decimal places might seem more accurate, but can be unnecessary and even misleading.
Alternative Methods for Conversion
While the core method is the most direct, alternative approaches can be useful depending on the specific fraction and your mathematical comfort level.
-
Finding an equivalent fraction with a denominator of 100: This method works best when the denominator is a factor of 100 (or easily manipulated to become one). Unfortunately, 12 is not a direct factor of 100. However, understanding this method is valuable for fractions where it is applicable. For example, converting 25/100 is trivial; it's directly 25%.
-
Using a calculator: Most calculators have built-in functionality for fraction-to-decimal and decimal-to-percentage conversions. This can streamline the process, especially for more complex fractions.
Practical Applications and Real-World Examples
The ability to convert fractions to percentages is crucial in numerous real-world situations:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates all involve working with percentages. Understanding fraction-to-percentage conversion is essential for interpreting financial statements and making informed financial decisions.
-
Statistics: Percentages are extensively used to present data and probabilities. Converting fractions representing proportions to percentages makes it easier to understand and communicate statistical findings.
-
Measurement and Engineering: Percentages are frequently used to represent tolerances, errors, or efficiency levels in engineering and construction projects.
-
Everyday Life: Understanding percentages is beneficial for calculating tips, discounts in stores, and even for understanding election results presented as percentages of votes cast.
Expanding the Concept: Working with More Complex Fractions
The principle of converting fractions to percentages remains the same even with more complex fractions, involving mixed numbers or improper fractions:
-
Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 2 1/4). To convert, first transform it into an improper fraction (9/4 in this example), then follow the standard conversion steps.
-
Improper Fractions: An improper fraction has a numerator larger than the denominator (e.g., 7/4). This is perfectly acceptable; simply divide the numerator by the denominator to obtain the decimal, and then multiply by 100 to find the percentage.
Example with a Mixed Number:
Let's convert the mixed number 1 1/8 to a percentage:
-
Convert to an improper fraction: 1 1/8 = (1 x 8 + 1) / 8 = 9/8
-
Convert to a decimal: 9 ÷ 8 = 1.125
-
Convert to a percentage: 1.125 x 100 = 112.5%
Addressing Common Mistakes and Challenges
-
Order of operations: Remember to divide the numerator by the denominator before multiplying by 100. Doing it in the wrong order will lead to an incorrect answer.
-
Rounding errors: Be mindful of the level of precision required and round appropriately. Over-rounding or under-rounding can affect the accuracy of your calculations.
-
Interpreting the result: Understand that percentages represent a proportion out of 100. A percentage greater than 100% signifies that the fraction represents a value greater than one whole.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill with wide-ranging applications. By understanding the core method, exploring alternative approaches, and practicing with different examples (including mixed and improper fractions), you can build confidence and proficiency in this essential mathematical concept. Remember to pay attention to rounding and the context of your calculations to ensure accuracy and meaningful interpretation of your results. This comprehensive guide aims to equip you with the knowledge and understanding needed to confidently tackle fraction-to-percentage conversions in any situation.
Latest Posts
Latest Posts
-
How Many Inches In 1 8 Metres
Apr 18, 2025
-
How Many Centimeters In 6 Meters
Apr 18, 2025
-
What Are The Factors For 2
Apr 18, 2025
-
Is Malleable A Chemical Or Physical Property
Apr 18, 2025
-
25 Cm Is Equal To How Many Inches
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 5/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.