What Is The Percentage Of 12/20
Kalali
Mar 26, 2025 · 5 min read
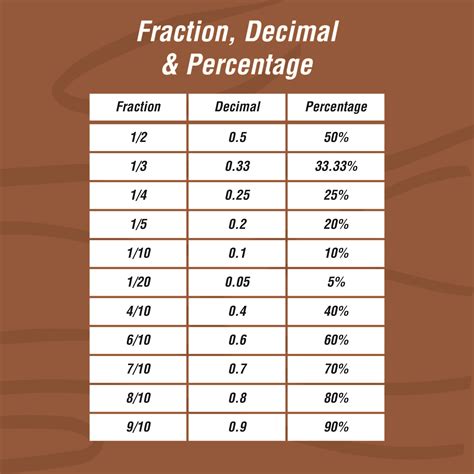
Table of Contents
What is the Percentage of 12/20? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine percentages not only enhances your mathematical abilities but also empowers you to confidently interpret data presented in percentage formats. This article will delve into the specifics of calculating the percentage represented by the fraction 12/20, explaining the method and providing context to broaden your understanding of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are used extensively because they provide a standardized way to compare different quantities, even if those quantities are expressed in different units or scales.
Calculating the Percentage of 12/20
The fraction 12/20 represents 12 parts out of a total of 20 parts. To convert this fraction into a percentage, we need to express it as a fraction with a denominator of 100. There are two primary methods to achieve this:
Method 1: Using Equivalent Fractions
This method involves finding an equivalent fraction for 12/20 where the denominator is 100. We can do this by finding a number that, when multiplied by 20, equals 100. That number is 5 (because 20 x 5 = 100). Crucially, whatever we multiply the denominator by, we must also multiply the numerator by the same number to maintain the fraction's value.
Therefore:
(12/20) x (5/5) = 60/100
Since 60/100 means 60 out of 100, this fraction is equivalent to 60%.
Method 2: Using Decimal Conversion
This method involves first converting the fraction 12/20 into a decimal by dividing the numerator (12) by the denominator (20).
12 ÷ 20 = 0.6
To convert this decimal to a percentage, we multiply it by 100 and add the percentage symbol (%):
0.6 x 100 = 60%
Therefore, using this method also confirms that 12/20 is equivalent to 60%.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is vital for various everyday scenarios:
1. Academic Performance:
Imagine a student scored 12 out of 20 on a test. Knowing that this equates to 60% allows for easy comparison with other scores and helps gauge their overall performance.
2. Financial Matters:
- Discounts: A store offers a 20% discount on an item priced at $100. Calculating the discount (20% of $100 = $20) and the final price ($100 - $20 = $80) is crucial for informed purchases.
- Interest Rates: Understanding interest rates, whether on savings accounts or loans, requires the ability to calculate percentages. For example, a 5% annual interest on a $1000 investment means earning $50 in interest after one year.
- Taxes: Calculating taxes payable involves determining a percentage of income or purchase value.
3. Data Analysis and Interpretation:
Percentages are extensively used to represent data in charts, graphs, and reports. Understanding percentages makes it easier to interpret statistical information and draw meaningful conclusions. For example, understanding market share often requires analyzing percentages.
4. Everyday Budgeting and Spending:
Tracking your spending involves calculating percentages of your income allocated to different expenses (e.g., housing, food, transportation). This helps manage your finances efficiently.
5. Scientific and Research Applications:
In scientific research and data analysis, percentages are frequently used to present findings and draw inferences. For instance, expressing experimental success rates or the prevalence of a specific characteristic within a population often uses percentages.
Advanced Percentage Calculations: Beyond the Basics
While the calculation of 12/20 as 60% is relatively straightforward, understanding percentage calculations extends to more complex scenarios:
1. Calculating Percentage Increase or Decrease:
This involves determining the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] x 100%
For example, if a product's price increased from $50 to $60, the percentage increase would be:
[(60 - 50) / 50] x 100% = 20%
2. Finding a Percentage of a Number:
To find a percentage of a given number, convert the percentage to a decimal and multiply it by the number. For example, finding 30% of 200:
0.30 x 200 = 60
3. Determining the Original Value from a Percentage:
If you know the final value after a percentage increase or decrease, you can work backward to find the original value. This frequently involves using algebraic techniques.
4. Working with Multiple Percentages:
In more complex scenarios, you might need to work with multiple percentages consecutively. This requires a careful and step-by-step approach. For instance, calculating compound interest involves applying a percentage repeatedly over time.
Tips for Accurate Percentage Calculations
- Double-check your work: Always verify your calculations to ensure accuracy.
- Use a calculator: For complex calculations, a calculator can help avoid errors.
- Practice regularly: The more you practice, the more proficient you'll become in calculating percentages.
- Understand the context: The meaning and interpretation of a percentage are highly dependent on the context in which it's used. Always consider the units and the overall meaning of the numbers involved.
Conclusion
Calculating the percentage of 12/20, which equals 60%, is a simple yet fundamental application of percentage calculations. Mastering this skill opens doors to a wide range of applications across various aspects of life, from personal finance to professional endeavors. Understanding the methods involved, along with the diverse contexts in which percentage calculations are utilized, empowers individuals to interpret data effectively and make informed decisions. Remember to practice regularly and always double-check your work to ensure accuracy. By consistently applying these skills, you'll confidently navigate the world of percentages and enhance your numeracy skills significantly.
Latest Posts
Latest Posts
-
How Many Feet Are In 63 Inches
Mar 29, 2025
-
Is The Knee Proximal To The Ankle
Mar 29, 2025
-
What Is 15 Percent Of 120
Mar 29, 2025
-
Cuanto Es 200 Grados Centigrados En Farenheit
Mar 29, 2025
-
What Is 17 Out Of 20
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 12/20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
