What Is The Percentage Of 2 Out Of 15
Kalali
Apr 25, 2025 · 5 min read
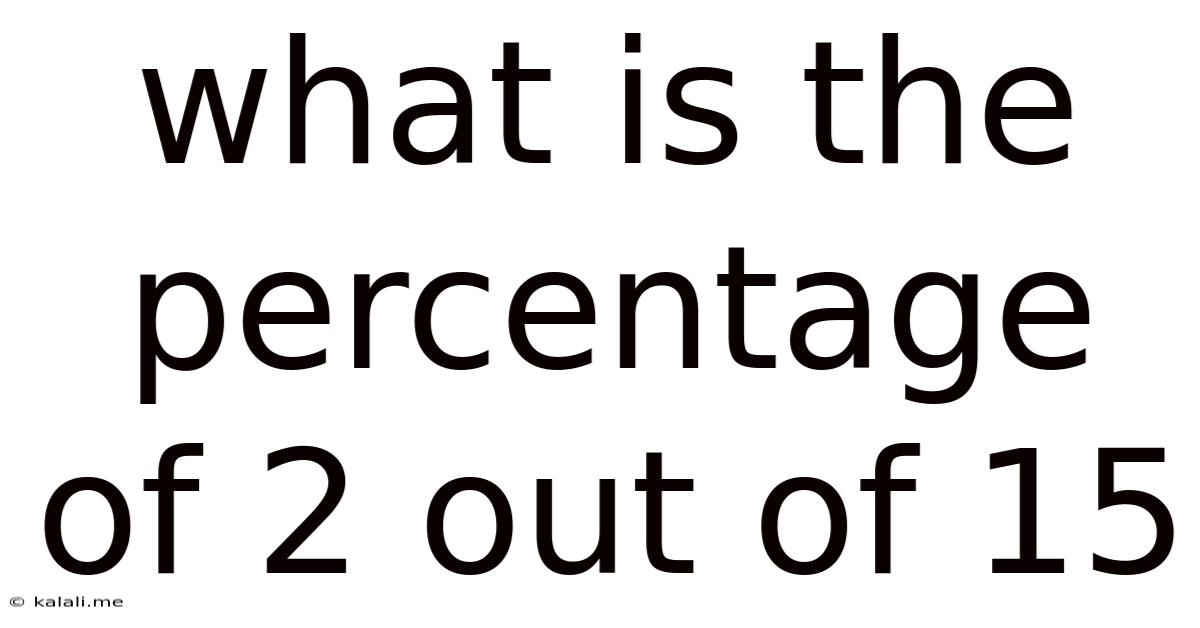
Table of Contents
What is the Percentage of 2 out of 15? A Deep Dive into Percentage Calculations and Their Applications
Calculating percentages is a fundamental skill with widespread applications across various fields, from everyday budgeting and shopping to complex statistical analysis and scientific research. Understanding how to determine the percentage of a part relative to a whole is crucial for making informed decisions and interpreting data effectively. This article will explore the calculation of "what is the percentage of 2 out of 15," delving into the process, providing different calculation methods, and illustrating its relevance in various real-world scenarios. We'll also touch upon advanced percentage-related concepts and their practical implications.
Meta Description: Learn how to calculate the percentage of 2 out of 15. This comprehensive guide covers various methods, real-world applications, and advanced percentage concepts for a complete understanding.
Understanding Percentages: The Basics
A percentage represents a fraction of 100. It expresses a proportion or ratio as a number out of 100. The symbol "%" denotes percentage. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Calculating percentages involves finding the ratio of a part to the whole and then expressing that ratio as a number out of 100.
Calculating the Percentage of 2 out of 15: The Primary Method
The most straightforward method to determine the percentage of 2 out of 15 involves a simple three-step process:
-
Formulate the Fraction: Express the problem as a fraction. In this case, the fraction is 2/15 (2 is the part, and 15 is the whole).
-
Convert the Fraction to a Decimal: Divide the numerator (2) by the denominator (15). 2 ÷ 15 ≈ 0.1333
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%). 0.1333 x 100 ≈ 13.33%
Therefore, 2 out of 15 represents approximately 13.33%.
Alternative Calculation Methods
While the primary method is the most common and easily understood, alternative approaches can offer different perspectives and enhance understanding:
-
Using Proportions: We can set up a proportion: 2/15 = x/100. Solving for x (the percentage) involves cross-multiplication: 15x = 200. Dividing both sides by 15, we get x ≈ 13.33%.
-
Using a Calculator: Most calculators have a percentage function. Simply input 2 ÷ 15 and then multiply the result by 100 to obtain the percentage.
-
Mental Estimation: For quick estimations, you can round the numbers. For example, thinking of 2 out of 15 as approximately 2 out of 20 simplifies to 10%. This provides a reasonable approximation, particularly useful in situations requiring quick calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in many real-world contexts:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely on percentage calculations. Understanding percentage changes helps track financial performance and make informed investment decisions. For example, determining the percentage increase or decrease in your savings account balance relies heavily on this fundamental calculation.
-
Retail and Sales: Sales discounts (e.g., a 20% off sale), calculating the final price after applying a discount, or determining the markup percentage on goods are crucial aspects of retail operations and sales strategies. A shop owner might use these calculations to assess profit margins based on the cost price and selling price of goods.
-
Science and Statistics: Percentages are extensively used in statistical analysis, representing proportions in data sets, expressing probabilities, and summarizing research findings. For example, understanding the percentage of respondents who agreed with a survey question is fundamental to interpreting the results of market research.
-
Education: Calculating grades, assessing student performance, and determining class averages all involve working with percentages. Teachers commonly use this calculation to express student progress as a percentage of total marks available.
-
Health and Medicine: Expressing the success rate of treatments, calculating the prevalence of diseases within a population, and describing the efficacy of medication utilize percentages effectively. Analyzing the recovery rate of patients after a treatment is another practical example.
-
Everyday Life: Tips at restaurants, determining the percentage of ingredients in a recipe, or calculating sales tax are all commonplace applications of percentage calculations. Even calculating a discount percentage when you are shopping for groceries is an important life skill.
Advanced Percentage Concepts
Beyond basic percentage calculations, understanding more advanced concepts further enhances your analytical skills:
-
Percentage Change: This involves calculating the increase or decrease in a value as a percentage of the original value. The formula is: [(New Value - Original Value) / Original Value] x 100.
-
Percentage Point Difference: This is often confused with percentage change. It refers to the simple difference between two percentages. For example, if a value increases from 10% to 15%, the percentage point difference is 5, not 50% (which would be the percentage change).
-
Compound Interest: This is the interest earned on both the principal amount and accumulated interest. It's a crucial concept in finance and investment planning, particularly long-term investments where interest is compounded periodically.
-
Weighted Averages: These are averages where different values contribute differently to the final result, often weighted by percentages. This is vital in many statistical applications.
Error Analysis and Precision
It's important to be mindful of rounding errors when working with percentages. In the case of 2 out of 15, we obtained 13.33%. This is an approximation; the exact decimal representation is a recurring decimal. Depending on the context, you might need to round to a specific number of decimal places for accuracy. For instance, in financial calculations, you may need to be precise to several decimal places, whereas in other contexts, rounding to the nearest whole percentage is sufficient.
Conclusion
Calculating the percentage of 2 out of 15, resulting in approximately 13.33%, is a simple yet crucial calculation with broad applications across numerous fields. Mastering percentage calculations, including both basic methods and advanced concepts, is essential for effective decision-making, data interpretation, and problem-solving in diverse real-world scenarios. Understanding the nuances of percentage calculations, particularly rounding errors and the differences between percentage change and percentage point difference, ensures accuracy and precision in your analyses. Continuous practice and application of these concepts will solidify your understanding and improve your analytical capabilities. The ability to confidently calculate and interpret percentages is a valuable skill that enhances both personal and professional competence.
Latest Posts
Latest Posts
-
10 Oz Of Water Is How Many Cups
Apr 25, 2025
-
Angle Elevation And Depression Word Problems
Apr 25, 2025
-
How Many Ounces Are In 200 Grams
Apr 25, 2025
-
At Room Temperature Most Metals Are
Apr 25, 2025
-
How Much Is 200 Ml Water In Cups
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 2 Out Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.