What Is The Percentage Of 3/2
Kalali
Mar 11, 2025 · 5 min read
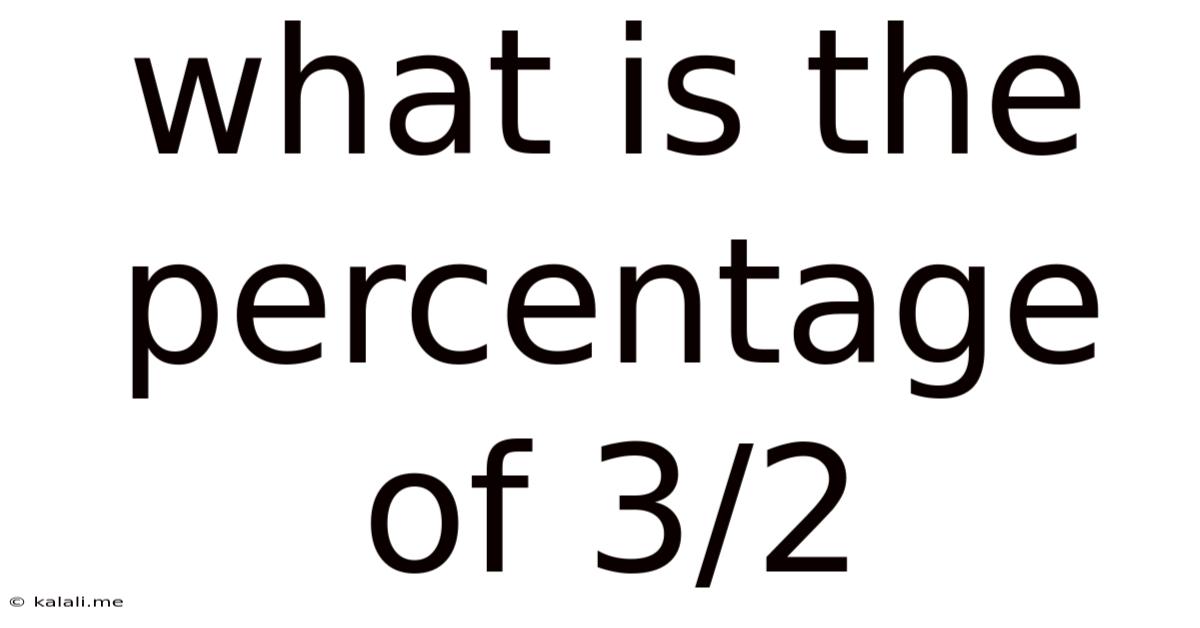
Table of Contents
What is the Percentage of 3/2? Understanding Fractions and Percentages
The question "What is the percentage of 3/2?" might seem deceptively simple at first glance. However, it opens the door to understanding the fundamental relationship between fractions and percentages, a crucial concept in mathematics and various real-world applications. This comprehensive guide will not only answer the question directly but also delve into the underlying principles, providing you with a robust understanding of how to convert fractions to percentages and vice-versa.
From Fractions to Percentages: A Step-by-Step Guide
A fraction represents a part of a whole. The fraction 3/2, also known as an improper fraction (where the numerator is larger than the denominator), indicates that we have more than one whole. To express this as a percentage, we need to convert it to a decimal and then multiply by 100.
Here's the breakdown:
-
Convert the fraction to a decimal: To do this, we simply divide the numerator (3) by the denominator (2): 3 ÷ 2 = 1.5
-
Multiply the decimal by 100: This step transforms the decimal into a percentage. 1.5 x 100 = 150
Therefore, 3/2 is equal to 150%.
Understanding the Significance of 150%
A percentage greater than 100% signifies that we have more than the whole. In this case, 150% represents one and a half times the original whole. Imagine you had a jar filled to its capacity (100%). If you were to add half more of the same amount of contents, you'd reach 150% of the jar's original capacity.
This concept is crucial in various scenarios:
- Financial Growth: If your investments increase by 150%, it means they have more than doubled in value.
- Sales and Marketing: A 150% increase in sales indicates significantly higher performance compared to the previous period.
- Data Analysis: In statistical analysis, percentages exceeding 100% can represent growth, exceeding expectations, or other significant trends.
Further Exploration of Fractions and Percentages
Let's explore additional facets of this essential mathematical relationship:
Different Types of Fractions
Understanding the different types of fractions is crucial for accurate conversion to percentages. We've already encountered an improper fraction (3/2). Other types include:
-
Proper Fractions: The numerator is smaller than the denominator (e.g., 1/2, 2/5). These always result in percentages less than 100%.
-
Mixed Numbers: These combine a whole number and a proper fraction (e.g., 1 1/2). To convert these to percentages, first convert the mixed number into an improper fraction, then follow the steps outlined above. For instance, 1 1/2 becomes 3/2, which, as we've established, equals 150%.
-
Equivalent Fractions: Fractions that represent the same value but have different numerators and denominators (e.g., 1/2 = 2/4 = 3/6). No matter which equivalent fraction you choose, the resulting percentage will remain the same.
Converting Percentages to Fractions
The process is reversible. To convert a percentage to a fraction, follow these steps:
-
Divide the percentage by 100: This removes the percentage symbol and converts the value to a decimal.
-
Simplify the resulting decimal into a fraction: This involves finding the simplest form of the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD).
For example, let's convert 75% to a fraction:
-
75% ÷ 100 = 0.75
-
0.75 can be expressed as the fraction 75/100. The GCD of 75 and 100 is 25. Dividing both by 25 simplifies the fraction to 3/4.
Practical Applications: Real-World Examples
The ability to convert between fractions and percentages is invaluable in many practical situations:
-
Calculating Discounts: If a store offers a 25% discount, you can quickly calculate the savings by converting 25% to the fraction 1/4 and multiplying it by the original price.
-
Understanding Interest Rates: Understanding interest rates, whether for loans or savings accounts, requires converting percentages to decimals or fractions for accurate calculations.
-
Analyzing Data: In various fields like finance, healthcare, and market research, data is often presented as percentages. The ability to convert these percentages back to fractions provides a deeper understanding of the underlying proportions.
-
Recipe Scaling: When adjusting recipes to serve more or fewer people, you might need to scale ingredients up or down by a certain percentage. Converting this percentage to a fraction or decimal makes the calculation easier.
-
Construction and Engineering: Percentages are frequently used in construction and engineering to express measurements and proportions. The ability to convert them to fractions aids in precise calculations.
Beyond the Basics: Advanced Concepts
For a more advanced understanding, you might explore these topics:
-
Percentage Change: This involves calculating the increase or decrease in a value over time, expressed as a percentage.
-
Compound Interest: This is interest calculated on the principal amount plus accumulated interest from previous periods. The understanding of percentages is critical for calculating compound interest accurately.
-
Statistical Analysis: Many statistical measures rely heavily on percentages, such as percentiles, which are used to divide a data set into equal parts.
Conclusion: Mastering Fractions and Percentages
The seemingly simple question, "What is the percentage of 3/2?", has led us on a journey through the interconnected world of fractions and percentages. Understanding the relationship between these concepts is not just a matter of mathematical proficiency; it's a crucial skill applicable to countless real-world scenarios. Whether you're dealing with financial calculations, data analysis, or everyday tasks, the ability to seamlessly convert between fractions and percentages empowers you to make accurate calculations, analyze data effectively, and solve problems with confidence. Remember, practice is key to mastering this essential skill. So, continue exploring different fractions and percentages, and soon, you'll find yourself confidently navigating the numerical landscape.
Latest Posts
Latest Posts
-
Why Did The Cow Want A Divorce
Jul 14, 2025
-
Lowest Common Denominator For 3 4 5
Jul 14, 2025
-
Can You Be A Professor With A Masters
Jul 14, 2025
-
How Many Bottles Of Water Is 1 Liter
Jul 14, 2025
-
How Many Days In A Million Minutes
Jul 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 3/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.