What Is The Percentage Of 3 Out Of 5
Kalali
Apr 08, 2025 · 6 min read
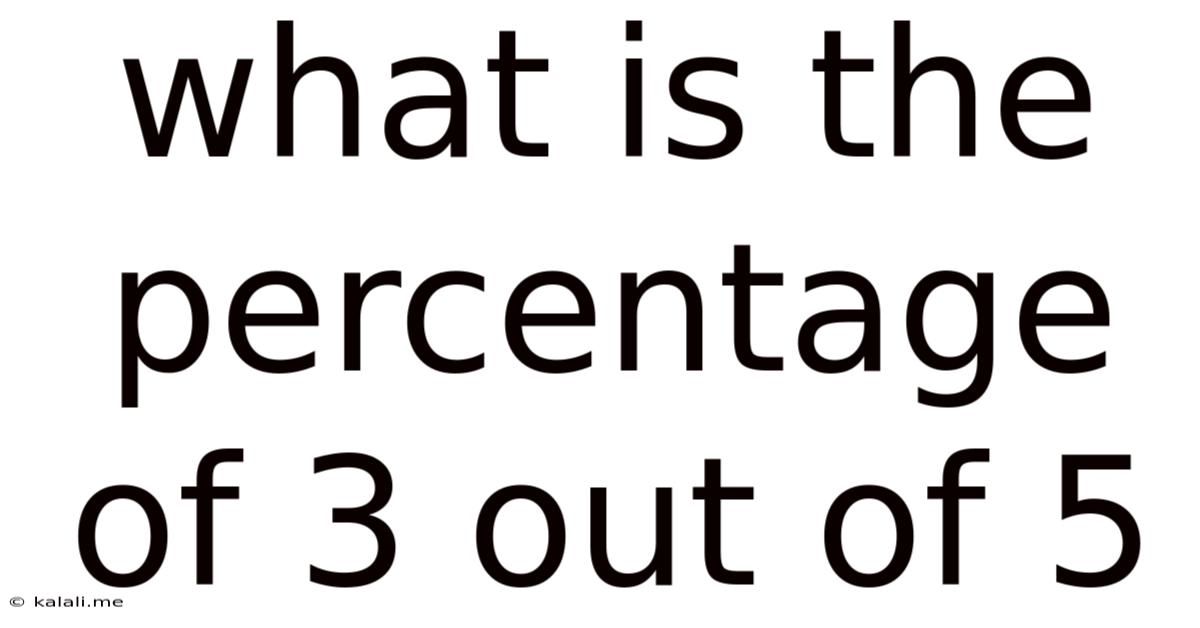
Table of Contents
What is the Percentage of 3 out of 5? A Deep Dive into Fractions, Ratios, and Percentages
This seemingly simple question – "What is the percentage of 3 out of 5?" – opens the door to a broader understanding of fundamental mathematical concepts. While the answer itself is straightforward, exploring the various methods of calculation and the underlying principles reveals a wealth of knowledge applicable to numerous scenarios in everyday life, from calculating discounts to understanding statistical data. This article will delve into the calculation, provide different approaches, and illustrate the significance of percentages in various contexts. We'll also address related concepts and potential misunderstandings.
Meta Description: Learn how to calculate the percentage of 3 out of 5, exploring different methods and understanding the underlying principles of fractions, ratios, and percentages. This comprehensive guide provides practical examples and addresses common misconceptions.
Understanding the Fundamentals: Fractions, Ratios, and Percentages
Before diving into the calculation, it's crucial to grasp the relationship between fractions, ratios, and percentages. These three concepts are interconnected and represent different ways of expressing the same proportional relationship.
-
Fraction: A fraction represents a part of a whole. In our case, 3 out of 5 is represented as the fraction 3/5. The numerator (3) represents the part, and the denominator (5) represents the whole.
-
Ratio: A ratio compares two or more quantities. The ratio of 3 out of 5 can be expressed as 3:5 (read as "3 to 5"). This signifies that for every 5 items, 3 possess a specific characteristic.
-
Percentage: A percentage expresses a fraction or ratio as a portion of 100. It's a convenient way to represent proportions and makes comparisons easier. The symbol "%" denotes "per cent" (out of 100).
Calculating the Percentage: Method 1 – Direct Conversion
The most straightforward method to determine the percentage of 3 out of 5 involves converting the fraction into a percentage directly. This involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (5): 3 ÷ 5 = 0.6
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol: 0.6 x 100 = 60%.
Therefore, 3 out of 5 is equal to 60%.
Calculating the Percentage: Method 2 – Proportion Method
The proportion method offers a more conceptual approach, particularly helpful for understanding the underlying relationships. This method sets up a proportion using the fraction and the percentage equivalent:
3/5 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
5x = 300
x = 300 ÷ 5
x = 60
Therefore, 3 out of 5 is 60%. This method clearly demonstrates the relationship between the fraction and its percentage equivalent.
Calculating the Percentage: Method 3 – Using a Calculator
Modern calculators simplify the process significantly. Simply enter "3 ÷ 5" and then multiply the result by 100. Most calculators will display the result directly as 60%. This is the fastest method for quick calculations but lacks the educational value of the previous two methods.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is essential in numerous real-world situations:
-
Discounts: Stores frequently offer discounts as percentages (e.g., 20% off). Calculating the final price after a discount requires percentage calculations.
-
Taxes: Sales tax is usually expressed as a percentage. Determining the total cost including tax involves adding the calculated percentage to the original price.
-
Interest Rates: Interest rates on loans and investments are expressed as percentages. Calculating the interest earned or paid requires understanding percentage calculations.
-
Statistical Data: Percentages are commonly used to represent statistical data, such as the percentage of people who voted for a particular candidate or the percentage of students who passed an exam. Interpreting such data necessitates understanding percentage calculations.
-
Grade Calculations: In many educational systems, grades are represented as percentages, reflecting the proportion of correct answers or achieved marks.
-
Financial Analysis: Investors and financial analysts frequently use percentages to analyze financial statements, comparing growth rates, profit margins, and other key financial metrics.
Common Misconceptions and Errors
While percentage calculations are relatively straightforward, some common misconceptions can lead to errors:
-
Confusing Percentage with Decimal: Failing to convert a decimal to a percentage (or vice versa) is a frequent mistake. Remember to multiply by 100 to convert a decimal to a percentage and divide by 100 to convert a percentage to a decimal.
-
Incorrectly Applying Percentages to Different Bases: Applying a percentage discount to a price that already includes the discount is a common error. Always ensure you are applying the percentage to the correct base value.
-
Misinterpreting Percentage Increases and Decreases: Sequential percentage increases or decreases do not simply add or subtract. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Ignoring the Context: The meaning of a percentage depends heavily on the context. A 10% increase in sales is very different from a 10% increase in unemployment. Always consider the context when interpreting percentage data.
Expanding the Knowledge: Beyond the Basics
The concept of "3 out of 5" can be expanded to explore more complex percentage calculations. Consider these examples:
-
Calculating Percentages of Larger Numbers: Applying the same principles, you can calculate the percentage of any number out of a larger total. For instance, what percentage is 15 out of 25? (Answer: 60%)
-
Calculating the Original Value: If you know a percentage and the resulting value, you can work backward to find the original value. For instance, if 60% of a number is 30, what is the original number? (Answer: 50)
-
Understanding Percentage Change: This involves comparing two values and calculating the percentage increase or decrease. For example, if sales increased from 100 to 120, what is the percentage increase? (Answer: 20%)
-
Working with Compound Percentages: Understanding how to work with compound percentages (e.g., compound interest) requires a deeper understanding of exponential growth and decay.
Conclusion: The Power of Percentage Understanding
The seemingly simple question of "What is the percentage of 3 out of 5?" serves as a gateway to understanding fundamental mathematical concepts crucial for navigating various aspects of life. By mastering the techniques of fraction, ratio, and percentage conversion, and by appreciating the potential pitfalls and nuanced applications, one gains a powerful tool applicable to countless situations – from personal finance to data analysis and beyond. The ability to confidently and accurately perform percentage calculations enhances both practical problem-solving skills and the capacity to critically interpret data presented in percentage form. This knowledge empowers informed decision-making in numerous contexts, making it a valuable skill worth cultivating.
Latest Posts
Latest Posts
-
How Many Hours Is 111 Minutes
Apr 17, 2025
-
How Much Is 1 3 Of A Pound
Apr 17, 2025
-
What Percent Is 45 Out Of 60
Apr 17, 2025
-
Which Refers To The Rate Of Change In Velocity
Apr 17, 2025
-
How Much Is 1 7 Oz In Ml
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 3 Out Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.