What Is The Percentage Of 40 Out Of 50
Kalali
Apr 16, 2025 · 5 min read
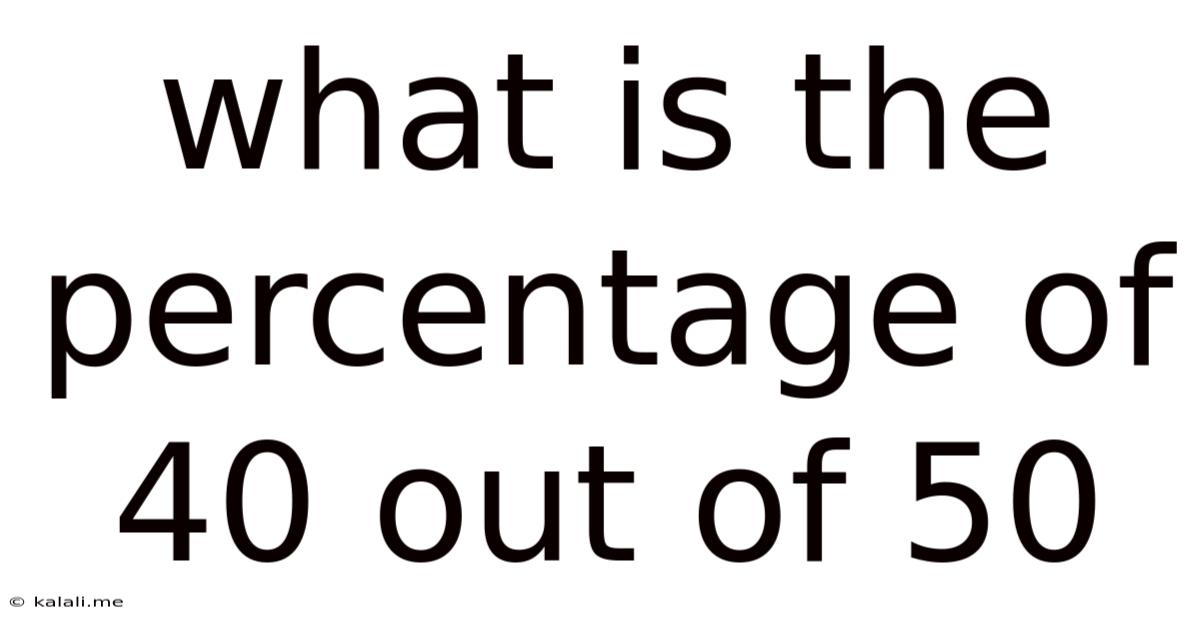
Table of Contents
What is the Percentage of 40 out of 50? A Deep Dive into Percentage Calculations and Applications
Calculating percentages is a fundamental skill in many aspects of life, from understanding financial reports and sales figures to grasping academic grades and sports statistics. This article will delve into the simple calculation of "What is the percentage of 40 out of 50?" and then expand on the broader concepts of percentage calculations, their real-world applications, and how to confidently tackle similar problems in the future. Understanding percentages is key to making informed decisions in various contexts, from personal finance to data analysis.
Understanding the Basics: Percentage Calculation
The core concept of a percentage is expressing a fraction or ratio as a portion of 100. The word "percent" literally means "out of 100" ("per" meaning "for each" and "cent" meaning "hundred"). Therefore, to find the percentage of 40 out of 50, we're essentially asking: "What fraction of 100 does 40 represent when compared to 50?"
Calculating the Percentage of 40 out of 50:
The most straightforward method involves a simple two-step process:
-
Find the fraction: Express the relationship between the two numbers as a fraction: 40/50.
-
Convert the fraction to a percentage: Multiply the fraction by 100%: (40/50) * 100% = 80%
Therefore, 40 out of 50 is 80%.
Different Methods for Percentage Calculation:
While the above method is the most direct, several other approaches can achieve the same result. These alternative methods are particularly helpful when dealing with more complex percentage problems:
-
Using Proportions: We can set up a proportion: 40/50 = x/100. Solving for 'x' (the percentage) gives us the same answer, 80%.
-
Decimal Conversion: First, convert the fraction 40/50 to a decimal by dividing 40 by 50: 40 ÷ 50 = 0.8. Then, multiply the decimal by 100%: 0.8 * 100% = 80%.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies this calculation. Simply enter 40 ÷ 50 %, and the calculator will directly give you the answer: 80%.
Real-World Applications of Percentage Calculations:
The ability to calculate percentages is crucial in a vast array of situations. Here are some examples:
-
Academic Performance: Grades are often expressed as percentages. If you scored 40 out of 50 on a test, understanding that this is an 80% translates your performance into a readily understandable metric.
-
Sales and Discounts: Retailers frequently advertise discounts as percentages. A "20% off" sale means you pay 80% of the original price. Calculating the final price requires understanding percentage calculations.
-
Financial Analysis: Investors use percentages to analyze financial statements, growth rates, and returns on investment. Understanding percentage change helps make informed investment decisions.
-
Data Analysis and Statistics: Percentages are extensively used in data analysis to represent proportions, probabilities, and trends within datasets. For example, survey results are often presented as percentages.
-
Sports Statistics: Batting averages, free throw percentages, and win percentages in sports are all expressed as percentages, providing a standardized way to compare player and team performance.
-
Tax Calculations: Income tax, sales tax, and other taxes are often calculated as a percentage of income or purchase price.
-
Tip Calculations: Determining the appropriate tip at a restaurant typically involves calculating a percentage (e.g., 15% or 20%) of the bill.
Expanding on Percentage Concepts: Percentage Increase and Decrease
Beyond simple percentage calculations, understanding percentage increase and decrease is equally important. These concepts are commonly used to represent changes over time or comparisons between values.
-
Percentage Increase: This refers to the increase in a value expressed as a percentage of the original value. The formula is: [(New Value - Original Value) / Original Value] * 100%.
-
Percentage Decrease: This represents the decrease in a value as a percentage of the original value. The formula is: [(Original Value - New Value) / Original Value] * 100%.
Example of Percentage Increase:
Let's say the price of a product increased from $50 to $60. The percentage increase is calculated as follows:
[(60 - 50) / 50] * 100% = 20%
Example of Percentage Decrease:
If the price of the same product later decreased from $60 to $48, the percentage decrease is:
[(60 - 48) / 60] * 100% = 20%
Advanced Percentage Problems and Solutions:
While calculating the percentage of 40 out of 50 is relatively straightforward, more complex problems might involve multiple steps or require a deeper understanding of percentage principles. Here's an example:
Problem: A store offers a 20% discount on an item priced at $100. After the discount, a 5% sales tax is added. What is the final price the customer pays?
Solution:
-
Calculate the discount: 20% of $100 = $20.
-
Calculate the discounted price: $100 - $20 = $80.
-
Calculate the sales tax: 5% of $80 = $4.
-
Calculate the final price: $80 + $4 = $84.
The final price the customer pays is $84.
Troubleshooting Common Mistakes in Percentage Calculations:
Several common mistakes can lead to inaccurate percentage calculations. Awareness of these errors can prevent miscalculations:
-
Incorrect Fraction Setup: Ensure the correct numbers are placed in the numerator (the number being expressed as a percentage) and the denominator (the total value).
-
Misinterpreting Percentage Changes: Clearly understand whether you're calculating a percentage increase or decrease, and use the correct formula.
-
Ignoring Order of Operations: When dealing with multiple steps, follow the order of operations (PEMDAS/BODMAS) correctly.
Conclusion:
Calculating percentages is an essential life skill applicable in diverse contexts. Understanding the fundamental principles, the various calculation methods, and potential pitfalls ensures accuracy and confidence in tackling percentage problems. The example of finding the percentage of 40 out of 50 serves as a foundation for understanding more complex percentage calculations, which are vital for informed decision-making across various domains, from personal finance to professional endeavors. Mastering percentages empowers individuals to better interpret data, analyze situations, and make more effective choices in their daily lives. This comprehensive guide provides a solid base for understanding and successfully applying percentage calculations in numerous real-world scenarios.
Latest Posts
Latest Posts
-
What Is 84 Inches In Centimetres
Apr 16, 2025
-
What Is 3 75 In A Fraction
Apr 16, 2025
-
When And Where Was Carbon Discovered
Apr 16, 2025
-
How Does A Metamorphic Rock Become An Igneous Rock
Apr 16, 2025
-
How Much Is 16 Inches In Feet
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 40 Out Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.