What Is The Percentage Of 5 7
Kalali
Apr 11, 2025 · 6 min read
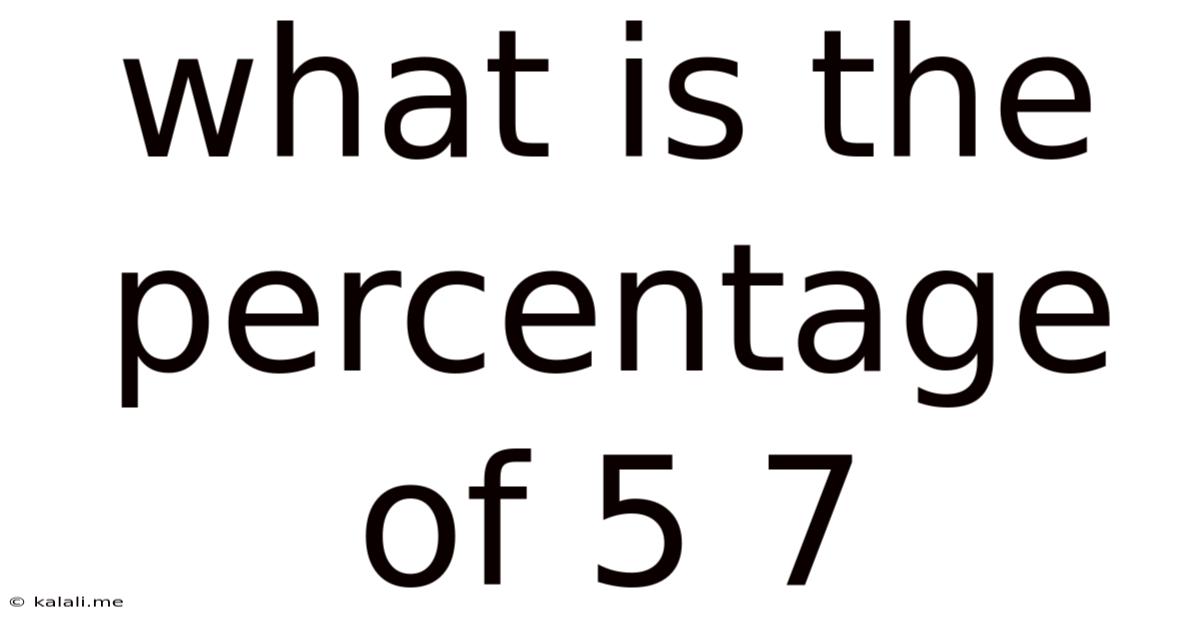
Table of Contents
What is the Percentage of 5 of 7? Understanding Fractions, Decimals, and Percentages
This seemingly simple question, "What is the percentage of 5 of 7?", opens the door to a deeper understanding of fundamental mathematical concepts: fractions, decimals, and percentages. While the answer itself is straightforward, exploring the various methods for calculating and interpreting the result provides valuable insight into mathematical relationships and practical applications. This article will not only provide the answer but also delve into the underlying principles, offering multiple approaches to solve this problem and similar percentage calculations. This will equip you with the tools to confidently tackle percentage problems in various contexts.
Meta Description: Learn how to calculate the percentage of 5 out of 7. This comprehensive guide explains fractions, decimals, and percentages, providing multiple methods for solving percentage problems and enhancing your mathematical understanding.
Understanding the Core Concepts
Before jumping into the calculation, let's clarify the three core concepts:
-
Fractions: A fraction represents a part of a whole. In this case, 5/7 represents 5 parts out of a total of 7 parts. The number above the line (5) is the numerator, and the number below the line (7) is the denominator.
-
Decimals: A decimal is a way of expressing a fraction using a base-10 system. It uses a decimal point to separate the whole number part from the fractional part. For instance, 0.5 represents one-half (1/2).
-
Percentages: A percentage is a fraction expressed as a portion of 100. The symbol "%" represents "per hundred" or "out of 100." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Direct Conversion from Fraction to Percentage
The most straightforward approach involves converting the fraction 5/7 into a percentage. This is achieved through a simple two-step process:
-
Convert the fraction to a decimal: Divide the numerator (5) by the denominator (7): 5 ÷ 7 ≈ 0.7142857
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol: 0.7142857 × 100 ≈ 71.43%
Therefore, 5 out of 7 is approximately 71.43%. The approximation is necessary because the decimal representation of 5/7 is non-terminating (it continues infinitely). Depending on the required level of precision, you can round the percentage to a suitable number of decimal places.
Method 2: Using Proportions
This method utilizes the concept of proportions to solve the problem. We can set up a proportion to find the percentage:
- 5/7 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
-
7x = 500
-
x = 500/7 ≈ 71.43
Again, this gives us approximately 71.43%. This method demonstrates the relationship between fractions and percentages, highlighting their proportional nature.
Method 3: Utilizing a Calculator
Modern calculators are equipped to handle percentage calculations directly. Most calculators have a percentage function (%) that simplifies the process. You can input the fraction (5/7) or the division (5 ÷ 7) and then multiply by 100 using the percentage function to obtain the result directly. This is often the quickest and most convenient method, especially for more complex percentage calculations.
Understanding the Significance of Rounding
As we've seen, the decimal representation of 5/7 is non-terminating. This means that the percentage will also be an approximation. The level of precision required will depend on the context of the problem. In many cases, rounding to two decimal places (71.43%) provides sufficient accuracy. However, in situations demanding higher precision, more decimal places might be necessary. Always consider the level of accuracy required before rounding your answer.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, tax amounts, and profit margins all rely on percentage calculations.
-
Statistics: Percentages are fundamental in presenting and analyzing data, showing proportions and trends.
-
Science: Many scientific calculations involve percentages, such as expressing concentrations of solutions or analyzing experimental data.
-
Everyday life: Understanding percentages helps us make informed decisions about shopping, budgeting, and many other aspects of daily life. For example, calculating sales tax, tips at restaurants, or understanding discount offers requires a firm grasp of percentages.
Beyond the Basics: Working with More Complex Percentages
The principles discussed above can be extended to more complex percentage problems. For instance, you might need to calculate percentage increase or decrease, or determine a percentage of a percentage. The key is to break down the problem into smaller, manageable steps, using the fundamental concepts of fractions, decimals, and percentages as your building blocks.
Advanced Percentage Calculations Examples
Let's consider a few more challenging percentage problems to illustrate the application of these principles:
Example 1: Percentage Increase
A product initially costs $100. The price increases by 15%. What is the new price?
-
Calculate the increase: 15% of $100 = (15/100) * $100 = $15
-
Add the increase to the original price: $100 + $15 = $115
Therefore, the new price is $115.
Example 2: Percentage Decrease
A shop offers a 20% discount on an item originally priced at $50. What is the discounted price?
-
Calculate the discount: 20% of $50 = (20/100) * $50 = $10
-
Subtract the discount from the original price: $50 - $10 = $40
The discounted price is $40.
Example 3: Percentage of a Percentage
A company increases its sales by 10% in the first quarter and then by another 5% in the second quarter. What is the total percentage increase over the two quarters?
This problem cannot be solved by simply adding the percentages (10% + 5% = 15%). Instead, we need to calculate the percentage increase step-by-step:
-
First-quarter increase: 10% increase on the original sales.
-
Second-quarter increase: 5% increase on the sales after the first-quarter increase.
Let's assume the original sales were $100.
-
First-quarter sales: $100 + (10% of $100) = $110
-
Second-quarter increase: 5% of $110 = $5.50
-
Total sales after two quarters: $110 + $5.50 = $115.50
-
Total percentage increase: (($115.50 - $100) / $100) * 100% = 15.5%
This example highlights the importance of understanding the order of operations when dealing with multiple percentage changes.
Conclusion
Calculating the percentage of 5 out of 7, while seemingly simple, provides a springboard for understanding the broader concepts of fractions, decimals, and percentages. Mastering these concepts is essential not only for academic success but also for navigating various aspects of daily life and professional endeavors. By understanding the different methods of calculation and the significance of rounding, you can confidently tackle percentage problems of varying complexities, making informed decisions and effectively analyzing data in diverse situations. Remember to break down complex problems into smaller, manageable steps, always paying attention to the level of precision required in your answer.
Latest Posts
Latest Posts
-
How Many Cans Of Soda Are In A 2 Liter
Jul 04, 2025
-
How Do U Say Of In Spanish
Jul 04, 2025
-
How Many Oz In A 10 Can
Jul 04, 2025
-
How Many Cups Is 16 Ounces Of Peanut Butter
Jul 04, 2025
-
How Many Square Feet Are In One Yard
Jul 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 5 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.