What Is The Percentage Of 6/7
Kalali
Mar 14, 2025 · 5 min read
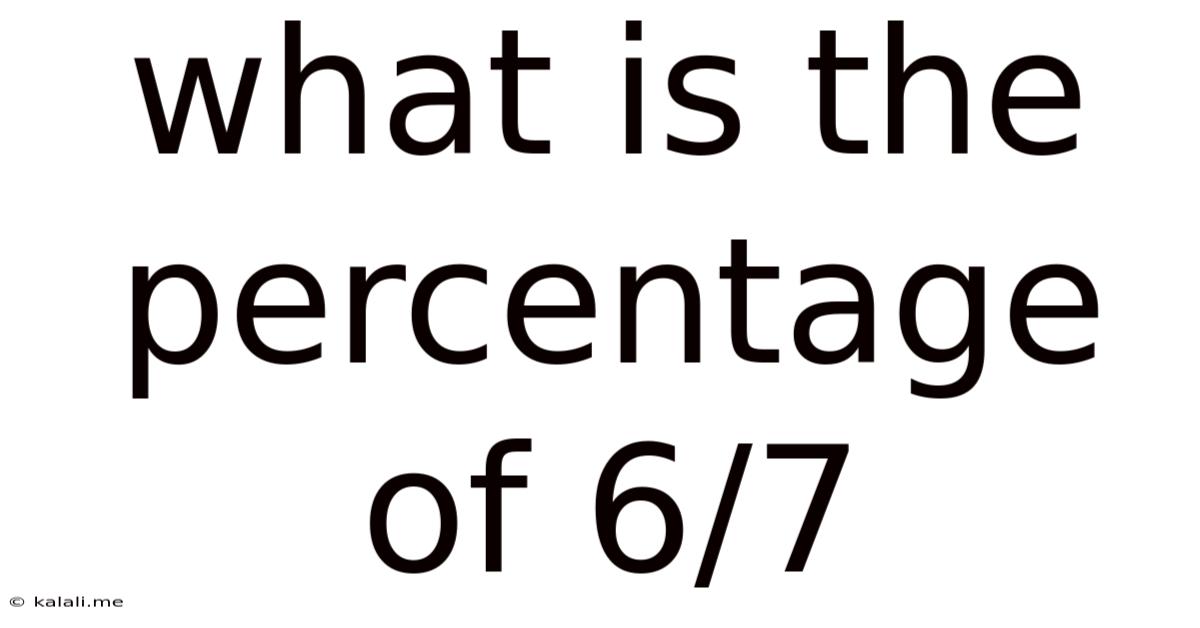
Table of Contents
What is the Percentage of 6/7? A Deep Dive into Fractions, Decimals, and Percentages
The seemingly simple question, "What is the percentage of 6/7?", opens a door to a deeper understanding of mathematical concepts crucial for everyday life and various professional fields. This article will not only answer the question directly but also explore the underlying principles of fractions, decimals, and percentages, providing you with a comprehensive toolkit to tackle similar problems confidently.
Understanding Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, 6/7 means 6 parts out of a total of 7 equal parts. The denominator defines the size of the whole, while the numerator indicates how many of those parts we're considering.
Converting Fractions to Decimals
To find the percentage equivalent of 6/7, we first need to convert the fraction into a decimal. This is done by dividing the numerator by the denominator:
6 ÷ 7 ≈ 0.8571428571
The result is an approximation, as 6/7 is a recurring decimal. This means the digits after the decimal point repeat infinitely (in this case, 857142). For most practical purposes, we'll round the decimal to a suitable number of decimal places. Rounding to four decimal places, we get 0.8571.
Converting Decimals to Percentages
A percentage is simply a fraction expressed as parts per hundred. To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol.
0.8571 x 100 = 85.71%
Therefore, 6/7 is approximately 85.71%.
Understanding Recurring Decimals and Their Significance
The recurring nature of the decimal representation of 6/7 highlights an important aspect of mathematical precision. While we've rounded to 85.71% for practical use, it's crucial to understand that this is an approximation. The true value retains its infinite repeating decimal sequence. This precision is essential in fields like engineering, finance, and scientific research where even minor inaccuracies can have significant consequences.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is essential in various real-world scenarios:
-
Calculating grades: If you answered 6 out of 7 questions correctly on a test, your score is approximately 85.71%.
-
Analyzing data: In business and statistics, representing data as percentages provides a clear and concise way to compare different proportions. For instance, if a company produced 6 out of 7 planned units, its production efficiency is roughly 85.71%.
-
Financial calculations: Percentages are fundamental in finance, used extensively for interest rates, discounts, profit margins, and tax calculations. Understanding fraction-to-percentage conversions allows for accurate financial computations.
-
Measurement and scaling: In fields like construction and design, converting fractions to percentages is vital for accurate scaling and measurements, ensuring projects are executed correctly.
Advanced Concepts: Working with Percentages and Fractions
Beyond the basic conversion, let's delve into more advanced concepts involving percentages and fractions:
-
Finding a percentage of a number: To find 85.71% of a number (let's say 100), we multiply the number by the decimal equivalent of the percentage: 100 x 0.8571 = 85.71.
-
Finding the original number from a percentage: If 85.71% of a number is 50, we can find the original number by dividing 50 by 0.8571: 50 ÷ 0.8571 ≈ 58.33.
-
Working with mixed numbers: If you have a mixed number like 1 6/7, you first convert it to an improper fraction (13/7) and then proceed with the decimal and percentage conversion as explained previously.
-
Comparing fractions using percentages: Converting fractions to percentages provides a straightforward way to compare fractions with different denominators. For instance, comparing 6/7 and 5/6 becomes easier when expressed as percentages (approximately 85.71% and 83.33%, respectively).
The Importance of Precision and Rounding
As we’ve seen with the recurring decimal of 6/7, precision is vital in mathematical computations. While rounding is often necessary for practical applications, understanding the limitations of rounding is equally important. In scenarios requiring high accuracy, using the unrounded decimal value or employing fractional calculations might be necessary to minimize errors. The choice of rounding precision depends heavily on the context and required level of accuracy.
Real-World Examples Illustrating Percentage Calculations
Let's examine several real-world examples where understanding percentage calculations based on fractions is crucial:
Example 1: Sales Performance
A salesperson aimed to meet a target of selling 7 units of a product. They sold 6 units. Their performance is calculated as (6/7) x 100% ≈ 85.71%. This percentage clearly shows that they almost achieved their target, offering valuable insight for performance evaluation and future goal setting.
Example 2: Project Completion
A construction project has 7 stages. 6 stages are complete. The project completion percentage is (6/7) x 100% ≈ 85.71%. This information is vital for project management, allowing stakeholders to monitor progress and make timely adjustments.
Example 3: Survey Results
In a survey of 7 respondents, 6 gave positive feedback. The positive feedback percentage is (6/7) x 100% ≈ 85.71%. This percentage is valuable in understanding public opinion and making informed decisions based on gathered feedback.
Example 4: Manufacturing Efficiency
A factory planned to produce 7 units of a product in a day. It actually produced 6. Its production efficiency is (6/7) x 100% ≈ 85.71%. This information is crucial for identifying potential bottlenecks and improving productivity.
Conclusion: Mastering Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill with broad applications in diverse fields. While the answer to "What is the percentage of 6/7?" is approximately 85.71%, the process of arriving at this answer provides a valuable learning experience, emphasizing the importance of precision, rounding, and the practical application of these mathematical concepts in daily life and professional settings. Mastering these conversions equips you with the tools to analyze data, solve problems, and make informed decisions across a wide spectrum of activities.
Latest Posts
Latest Posts
-
How Many Slices Of Turkey Is 3 Oz
Jul 06, 2025
-
Which Word Best Describes The Tone Of The Passage
Jul 06, 2025
-
How Long Does It Take To Count To One Billion
Jul 06, 2025
-
Why Did The Kangaroo See A Psychiatrist
Jul 06, 2025
-
How Long Would It Take To Walk To China
Jul 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 6/7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.