What Is The Percentage Of 9 Out Of 12
Kalali
Apr 10, 2025 · 5 min read
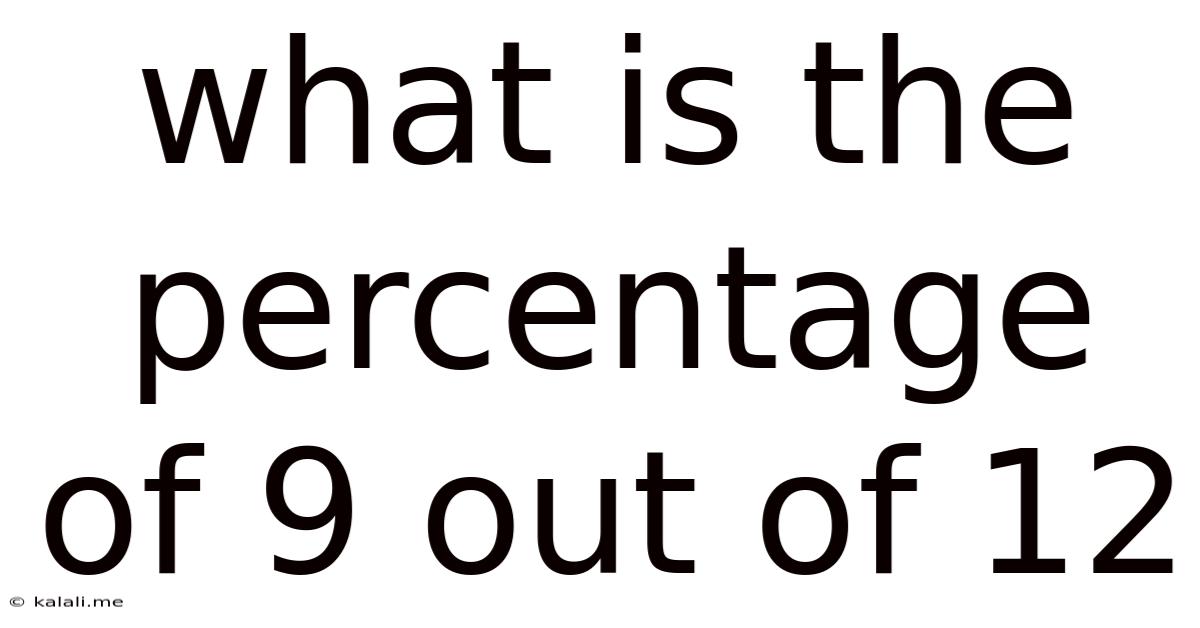
Table of Contents
What is the Percentage of 9 out of 12? A Deep Dive into Percentage Calculations and Applications
What is the percentage of 9 out of 12? This seemingly simple question opens the door to a broader understanding of percentages, their calculations, and their widespread applications in various fields. This article will not only answer the initial question but also explore the underlying principles, offer multiple calculation methods, and delve into practical examples demonstrating the importance of percentage calculations in everyday life and professional settings.
Meta Description: Learn how to calculate percentages effortlessly! This comprehensive guide explains how to find the percentage of 9 out of 12, explores different calculation methods, and demonstrates practical applications of percentages across various fields.
To answer the core question directly: 9 out of 12 represents 75%. But let's dissect this calculation and explore the various ways to arrive at this answer. Understanding the process is crucial, especially when dealing with more complex percentage problems.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Percentages are used to represent proportions, ratios, and changes in various contexts. They provide a standardized way to compare and understand different quantities.
For example, if you score 9 out of 12 on a test, it means you answered 9 questions correctly out of a total of 12. Expressing this as a percentage makes it easier to compare your performance with others or with previous attempts.
Method 1: The Direct Formula
The most straightforward way to calculate a percentage is using the following formula:
(Part / Whole) x 100% = Percentage
In our example:
(9 / 12) x 100% = 75%
This formula is universally applicable to all percentage calculations. Simply identify the "part" (the number you're expressing as a percentage) and the "whole" (the total number).
Method 2: Simplifying the Fraction
Before applying the formula, simplifying the fraction can make the calculation easier. In our case, 9/12 can be simplified:
9/12 = 3/4
Now, applying the formula:
(3 / 4) x 100% = 75%
This method is particularly useful when dealing with larger numbers or fractions that can be easily simplified.
Method 3: Using Decimal Conversion
Another approach involves converting the fraction to a decimal first and then multiplying by 100%:
9/12 = 0.75
0.75 x 100% = 75%
This method is often preferred when using a calculator, as it streamlines the process.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in numerous fields:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and returns on investments all rely heavily on percentages. Understanding percentage changes is crucial for analyzing financial performance. For instance, a 10% increase in sales can significantly impact a business's bottom line. Analyzing year-over-year percentage growth is a key metric for evaluating investment strategies and business growth.
-
Science: Percentages are frequently used to express concentrations of solutions, error margins in experiments, and statistical data analysis. For example, calculating the percentage of a certain element in a compound or determining the percentage of successful trials in an experiment are common scientific applications.
-
Education: Grade calculations, test scores, and performance evaluations often utilize percentages. Understanding your percentage score on an exam provides a clear measure of your comprehension. Similarly, universities use percentages extensively to communicate student progress and overall GPA (Grade Point Average).
-
Retail: Discounts and sales are always expressed as percentages. Knowing how to calculate these percentages quickly helps consumers make informed purchasing decisions. Retailers use percentage markups to calculate selling prices based on cost and desired profit margins.
-
Health: Doctors may use percentages to express the risk of certain health conditions, the effectiveness of treatments, or the percentage of body fat. Understanding these percentages helps patients make informed decisions about their healthcare.
Beyond the Basics: Calculating Percentage Increase and Decrease
While the core percentage calculation is straightforward, more complex scenarios involve percentage increases and decreases. Understanding these is crucial for analyzing changes in various quantities.
Percentage Increase:
The formula for calculating percentage increase is:
[(New Value - Old Value) / Old Value] x 100%
For example, if sales increased from 100 units to 120 units, the percentage increase is:
[(120 - 100) / 100] x 100% = 20%
Percentage Decrease:
The formula for calculating percentage decrease is:
[(Old Value - New Value) / Old Value] x 100%
For example, if the price of an item decreased from $100 to $80, the percentage decrease is:
[(100 - 80) / 100] x 100% = 20%
Working with Complex Percentage Problems
As you delve into more advanced applications, you'll encounter situations requiring multiple steps and a deeper understanding of percentage principles. These often involve combining different percentage calculations, such as calculating the final price after applying a series of discounts or calculating compound interest.
Utilizing Technology for Percentage Calculations
Spreadsheets (like Microsoft Excel or Google Sheets) and calculators are invaluable tools for performing percentage calculations, especially when dealing with large datasets or complex formulas. These tools offer built-in functions that simplify the process and reduce the risk of errors.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a fundamental skill with far-reaching applications. From everyday budgeting to complex financial analysis, mastering these calculations empowers you to make informed decisions, interpret data effectively, and navigate the numerical world with confidence. While the basic calculation of 9 out of 12 being 75% is a simple starting point, this article has explored the underlying principles, offered various calculation methods, and demonstrated the diverse and crucial applications of percentages in various fields. By understanding these concepts, you are well-equipped to tackle a wide range of percentage-related problems. Remember to always double-check your calculations and utilize available tools to ensure accuracy and efficiency.
Latest Posts
Latest Posts
-
How Many Degrees Is 200 Celsius
Apr 18, 2025
-
How Many Vertices Does A Trapezium Have
Apr 18, 2025
-
What Is The Highest Common Factor Of 20 And 30
Apr 18, 2025
-
What Is 230 Cm In Feet
Apr 18, 2025
-
Is Burning Physical Or Chemical Change
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 9 Out Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.