What Is The Percentage Of 9 Out Of 15
Kalali
Apr 16, 2025 · 5 min read
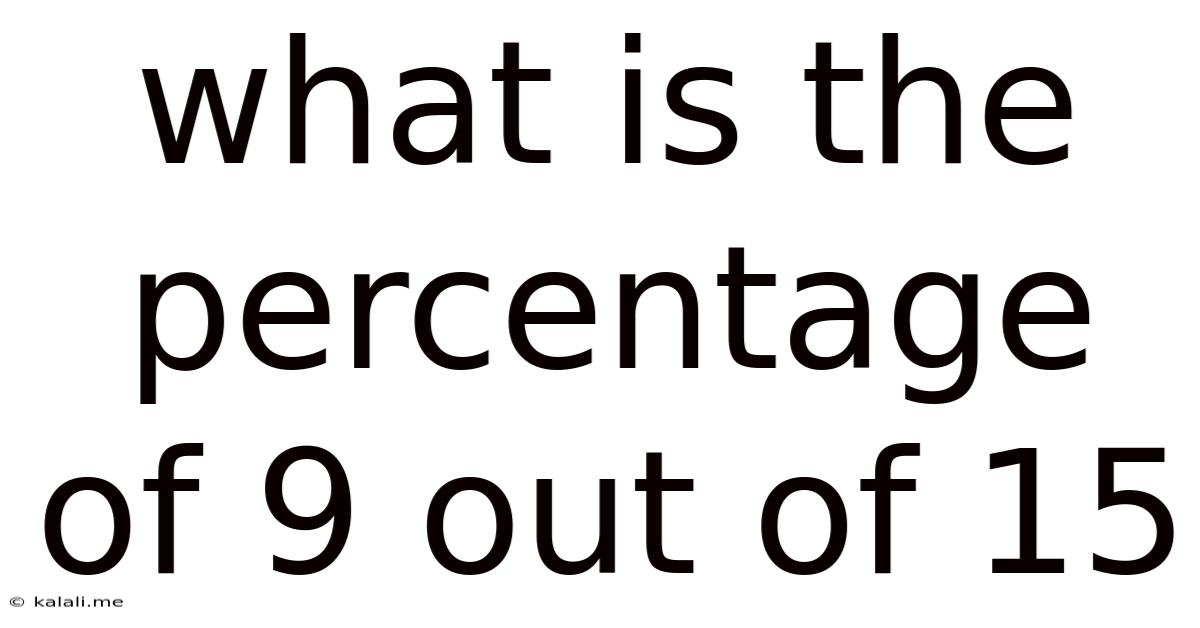
Table of Contents
What is the Percentage of 9 out of 15? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with broad applications across various fields, from everyday budgeting to complex scientific research. Understanding how to determine the percentage of one number relative to another is crucial for interpreting data, making comparisons, and drawing informed conclusions. This article will not only answer the question "What is the percentage of 9 out of 15?" but also delve into the underlying concepts, providing a comprehensive guide to percentage calculations and their practical use. We'll explore different methods, address common mistakes, and showcase real-world examples.
Meta Description: Learn how to calculate percentages! This in-depth guide explains how to find the percentage of 9 out of 15, covering various methods, common mistakes, and real-world applications. Master percentage calculations for everyday life and professional success.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used to represent proportions, ratios, and rates in a standardized and easily understandable format. They provide a convenient way to compare different quantities and visualize changes over time.
Calculating the Percentage of 9 out of 15: Three Methods
There are several ways to calculate the percentage of 9 out of 15. Let's explore three common methods:
Method 1: Using the Fraction Method
This is perhaps the most intuitive method. We can represent "9 out of 15" as a fraction: 9/15. To convert this fraction to a percentage, we need to express it as a fraction with a denominator of 100. We can do this by dividing 9 by 15 and then multiplying the result by 100:
(9/15) * 100 = 0.6 * 100 = 60%
Therefore, 9 out of 15 is 60%.
Method 2: Using Decimal Conversion
This method involves first converting the fraction to a decimal and then multiplying by 100. Again, starting with the fraction 9/15:
9 ÷ 15 = 0.6
Now, multiply the decimal by 100 to express it as a percentage:
0.6 * 100 = 60%
This method is efficient and straightforward, particularly when dealing with fractions that easily convert to decimals.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the unknown percentage. We can set up a proportion as follows:
9/15 = x/100
Where 'x' represents the percentage we want to find. To solve for x, we cross-multiply:
15x = 900
x = 900/15
x = 60
Therefore, x = 60%, confirming our previous calculations. This method is particularly useful when dealing with more complex percentage problems.
Common Mistakes to Avoid When Calculating Percentages
While percentage calculations are relatively straightforward, several common mistakes can lead to inaccurate results. Here are some points to keep in mind:
-
Incorrect Fraction Formation: Ensure the fraction accurately represents the problem. For example, "9 out of 15" must be written as 9/15, not 15/9.
-
Order of Operations: When using the formula (part/whole) * 100, ensure the division is performed before the multiplication.
-
Decimal Point Errors: Be careful when converting decimals to percentages. Remember to multiply by 100, not just move the decimal point.
-
Rounding Errors: Depending on the context, you may need to round the percentage to a specific number of decimal places. However, avoid premature rounding during intermediate calculations, as this can lead to inaccuracies in the final result.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous everyday situations and professional contexts. Here are some examples:
-
Finance: Calculating interest rates, discounts, tax percentages, profit margins, and investment returns all involve percentage calculations. Understanding percentage changes helps in tracking financial performance and making informed financial decisions. For example, determining the percentage increase or decrease in your monthly expenses or investment portfolio requires a solid grasp of percentage calculations.
-
Retail and Sales: Sales discounts, markups, and profit margins are all expressed as percentages. Retailers use percentages to calculate price reductions during sales, determine profit on individual items, and analyze overall profitability. Understanding these calculations is crucial for effective pricing strategies and sales management.
-
Science and Statistics: Percentages are widely used in scientific research to represent data, analyze trends, and present findings. Statistical analysis frequently involves calculating percentages to describe proportions, distributions, and changes in variables.
-
Education: Grade calculations, test scores, and performance evaluations often rely on percentages. Students and educators alike use percentages to track academic progress and identify areas for improvement.
-
Healthcare: Many healthcare metrics are represented as percentages. For instance, calculating the success rate of a medical procedure or the prevalence of a particular disease in a population involves percentage calculations.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of completion of a project, or comparing prices of different products all use percentages. These are simple yet essential calculations that simplify our daily lives.
Beyond the Basics: More Complex Percentage Problems
While calculating the percentage of 9 out of 15 is a relatively simple exercise, more complex percentage problems may require a deeper understanding of the concepts involved. For instance, you may need to calculate percentage increases or decreases, find the original value after a percentage change, or solve problems involving multiple percentage changes. These advanced problems often necessitate a good understanding of algebraic equations and the ability to manipulate formulas to isolate the unknown variable.
Conclusion: Mastering Percentage Calculations
Calculating percentages is a fundamental mathematical skill that finds applications in various aspects of life. Understanding the different methods for calculating percentages and avoiding common mistakes ensures accurate and reliable results. Mastering percentage calculations not only aids in problem-solving but also empowers individuals to make informed decisions in personal finance, professional fields, and everyday life. By embracing a thorough understanding of percentage calculations, you equip yourself with a powerful tool for navigating the complexities of the numerical world. The seemingly simple question of "What is the percentage of 9 out of 15?" thus becomes a gateway to a broader understanding of mathematical concepts and their real-world significance. Through consistent practice and the application of different methods, you can build confidence and proficiency in this essential skill.
Latest Posts
Latest Posts
-
What Is The Diameter Of A Quarter
Jul 02, 2025
-
Spoon Gets Hot In A Bowl Of Soup
Jul 02, 2025
-
How Many Cups In A 16 Oz Sour Cream
Jul 02, 2025
-
How Many 1 4 Teaspoons Are In 1 Teaspoon
Jul 02, 2025
-
How Many Tbsp In A Dry Ounce
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 9 Out Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.