What Is The Probability Of Impossible Event
Kalali
Apr 06, 2025 · 6 min read
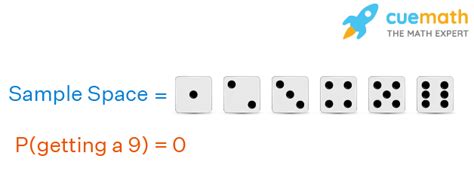
Table of Contents
What is the Probability of an Impossible Event? A Deep Dive into Probability Theory
The probability of an impossible event is a fundamental concept in probability theory that often sparks curiosity and requires a clear understanding. While seemingly straightforward, exploring this concept reveals deeper insights into the foundations of probability and its application in various fields. This article delves into the probability of impossible events, explaining its value and significance in both theoretical and practical contexts.
Understanding Probability and its Axioms
Before tackling the probability of impossible events, let's establish a solid foundation in probability theory. Probability quantifies the likelihood of an event occurring. It's expressed as a number between 0 and 1, inclusive:
- 0: Represents an impossible event – it will never occur.
- 1: Represents a certain event – it will always occur.
- Values between 0 and 1: Represent events with varying degrees of likelihood. A probability of 0.5 indicates an equal chance of the event occurring or not occurring.
Probability theory rests on three fundamental axioms:
- Non-negativity: The probability of any event is always greater than or equal to zero (P(A) ≥ 0).
- Normalization: The probability of the sample space (the set of all possible outcomes) is equal to one (P(S) = 1).
- Additivity: For any two mutually exclusive events A and B (meaning they cannot both occur simultaneously), the probability of either A or B occurring is the sum of their individual probabilities (P(A ∪ B) = P(A) + P(B)).
These axioms form the bedrock of all probability calculations and interpretations.
Defining an Impossible Event
An impossible event is an event that cannot occur under any circumstances. It's an event that lies outside the realm of possibility within the defined sample space. For instance:
- Rolling a 7 on a standard six-sided die: The die only has faces numbered 1 to 6; a 7 is not a possible outcome.
- Drawing a red ball from a bag containing only blue balls: The bag's contents exclude the possibility of drawing a red ball.
- The sun rising in the west tomorrow: Based on our understanding of celestial mechanics, this event is impossible.
The key characteristic is that there are zero favorable outcomes within the sample space for an impossible event.
The Probability of an Impossible Event: A Value of Zero
Given the axioms of probability and the definition of an impossible event, the probability of an impossible event is always 0. This aligns perfectly with the first axiom (non-negativity) and reflects the inherent impossibility. There are no occurrences that satisfy the conditions of the impossible event within the sample space.
Why is the Probability of Zero Important?
The assignment of probability 0 to an impossible event is not merely a mathematical formality; it has crucial implications:
- Completeness of Probability Models: Assigning a probability of 0 to impossible events ensures that the probability model is complete and accounts for all possible scenarios within the defined sample space. Every event, possible or impossible, has a defined probability.
- Logical Consistency: It maintains the logical consistency of the probability framework. If an impossible event were assigned a non-zero probability, it would contradict the basic axioms and lead to inconsistencies in probability calculations.
- Foundation for Conditional Probability: The probability of an impossible event serves as a crucial base case for conditional probability calculations. Conditional probability considers the likelihood of an event given that another event has already occurred. Understanding the probability of impossible events is critical for accurately computing conditional probabilities in complex scenarios.
- Application in Statistical Inference: In statistical hypothesis testing, the probability of an event under a null hypothesis helps determine whether to reject the hypothesis. The case of an impossible event helps to solidify this procedure.
- Real-World Applications: Consider risk assessment in engineering or finance. Identifying impossible events—scenarios that cannot realistically occur—is crucial for focusing resources on assessing and mitigating genuinely possible risks.
Contrasting Impossible Events with Events of Very Low Probability
It's vital to distinguish between an impossible event (probability 0) and an event with a very low probability (close to 0 but not exactly 0). While an impossible event will never occur, an event with a very low probability could theoretically occur, albeit with extremely low likelihood. The difference is fundamental:
- Impossible Event: Absolutely no chance of occurring.
- Very Low Probability Event: Extremely unlikely, but not impossible.
For instance, winning the lottery has a very low probability. It's improbable but not impossible. Conversely, rolling a 7 on a six-sided die is impossible. This distinction is critical for accurate risk assessment and decision-making.
Examples and Illustrations
Let's examine some real-world examples to further solidify this concept:
Example 1: Flipping a Coin
The sample space for flipping a fair coin is {Heads, Tails}. The probability of getting Heads is 0.5, and the probability of getting Tails is 0.5. The probability of getting a third outcome, such as "standing on its edge," is 0—it's an impossible event within the context of a standard coin flip.
Example 2: Drawing Cards from a Deck
Consider drawing a card from a standard deck of 52 playing cards. The probability of drawing a specific card (e.g., the Ace of Spades) is 1/52. The probability of drawing a card with a value of 14 is 0—there are no cards with a value of 14 in a standard deck.
Example 3: Weather Prediction
While weather prediction involves probabilities, certain events might be deemed impossible given existing conditions. For example, the probability of it snowing in the Sahara Desert in July (without artificial intervention) is practically 0, even though a tiny, non-zero probability exists theoretically.
Advanced Concepts and Applications
The concept of the probability of an impossible event extends to more advanced areas of probability theory, including:
- Measure Theory: In measure theory, a more rigorous mathematical framework for probability, the probability of an impossible event is defined as the measure of the empty set, which is 0.
- Conditional Probability and Bayes' Theorem: The probability of an impossible event is often used as a boundary condition in solving problems involving conditional probability and Bayes' Theorem, making it a building block of more complex analyses.
- Statistical Inference: Hypothesis testing relies on assessing the probability of observing data if a particular hypothesis is true. If the data would be impossible given the null hypothesis, then we are led to reject the null hypothesis.
Conclusion: The Importance of Zero
The probability of an impossible event, precisely 0, is not simply a mathematical detail. It's a cornerstone of probability theory, ensuring logical consistency and completeness. Understanding this concept is essential for correctly interpreting probabilities, constructing robust probability models, and making informed decisions across numerous fields where probability plays a crucial role. From everyday scenarios to complex scientific and engineering applications, the significance of an impossible event with its probability of zero underpins the reliability and usefulness of probability theory itself. The seemingly simple concept of the probability of an impossible event truly forms the bedrock upon which much of the field is built.
Latest Posts
Latest Posts
-
7 Of 20 As A Percentage
Apr 09, 2025
-
What Is The Percentage Of 4 Out Of 7
Apr 09, 2025
-
Lines Body Cavities And Covers The Bodys External Surface
Apr 09, 2025
-
How Many Ml Are In 12 Fl Oz
Apr 09, 2025
-
75 In Is How Many Feet
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Probability Of Impossible Event . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.