What Is The Reciprocal Of -2
Kalali
Apr 01, 2025 · 5 min read
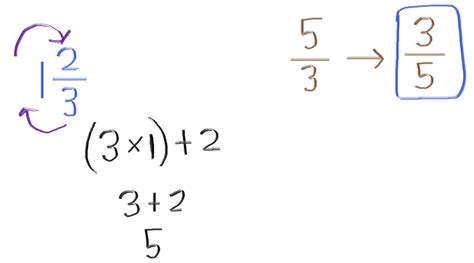
Table of Contents
What is the Reciprocal of -2? A Deep Dive into Mathematical Inverses
The seemingly simple question, "What is the reciprocal of -2?" opens a door to a fascinating exploration of fundamental mathematical concepts. While the answer itself is straightforward, understanding the underlying principles of reciprocals, their properties, and their applications provides a robust foundation for more advanced mathematical studies. This article will delve into the concept of reciprocals, focusing on the reciprocal of -2, and extending the discussion to include related topics and practical applications.
Understanding Reciprocals: The Multiplicative Inverse
The reciprocal of a number, also known as its multiplicative inverse, is the number that, when multiplied by the original number, results in a product of 1. In simpler terms, it's the number you need to multiply a given number by to get the multiplicative identity, which is 1.
Finding the Reciprocal: To find the reciprocal of any non-zero number 'x', you simply take 1 and divide it by 'x'. This can be expressed as 1/x or x⁻¹.
The Reciprocal of -2: Applying this principle to -2, the reciprocal is 1/(-2) or -1/2. When we multiply -2 by -1/2, we get:
(-2) * (-1/2) = 1
This confirms that -1/2 is indeed the reciprocal of -2.
Properties of Reciprocals
Reciprocals exhibit several key properties:
-
Every non-zero number has a reciprocal: This is a fundamental property. Zero, however, does not have a reciprocal because division by zero is undefined. This is because there is no number that, when multiplied by zero, results in 1.
-
The reciprocal of a reciprocal is the original number: This means that the reciprocal of -1/2 is -2. This is because (-1/2) * (-2) = 1.
-
The reciprocal of a positive number is positive: For instance, the reciprocal of 5 is 1/5.
-
The reciprocal of a negative number is negative: As demonstrated above, the reciprocal of -2 is -1/2.
-
The reciprocal of 1 is 1: This is because 1 * 1 = 1.
-
The reciprocal of -1 is -1: This is because (-1) * (-1) = 1.
Reciprocals in Different Number Systems
The concept of reciprocals extends beyond integers to other number systems, including rational numbers (fractions), irrational numbers (like π and √2), and complex numbers.
-
Rational Numbers: Finding the reciprocal of a fraction involves inverting the numerator and denominator. For example, the reciprocal of 2/3 is 3/2. Similarly, the reciprocal of -3/4 is -4/3.
-
Irrational Numbers: Irrational numbers also have reciprocals. The reciprocal of √2 is 1/√2, which can be rationalized to √2/2. The reciprocal of π is 1/π. These reciprocals are also irrational.
-
Complex Numbers: Complex numbers, which have a real and an imaginary part (a + bi, where 'i' is the imaginary unit, √-1), also possess reciprocals. The reciprocal of a complex number (a + bi) is found using complex conjugate division. The calculation can be intricate, but the result always exists except for the complex number 0 + 0i.
Applications of Reciprocals
Reciprocals play a crucial role in numerous mathematical and scientific applications:
-
Division: Division by a number is equivalent to multiplication by its reciprocal. For example, 6 ÷ 2 is the same as 6 * (1/2). This is a fundamental concept in algebra and arithmetic.
-
Solving Equations: Reciprocals are frequently used in solving algebraic equations. For example, to solve the equation 2x = 6, you multiply both sides by the reciprocal of 2 (which is 1/2), resulting in x = 3.
-
Matrix Algebra: In linear algebra, the inverse of a matrix is a crucial concept. The inverse matrix is analogous to the reciprocal of a number. It's used in solving systems of linear equations, among other applications.
-
Physics and Engineering: Reciprocals appear in many physical laws and engineering formulas. For example, in Ohm's law (V = IR), resistance (R) is the reciprocal of conductance (G).
Exploring Further: Advanced Concepts Related to Reciprocals
The concept of reciprocals naturally leads to further exploration of related mathematical concepts:
-
Inverse Functions: The reciprocal is a specific type of inverse. In general, an inverse function reverses the action of the original function. For a function to have an inverse, it must be one-to-one (injective) and onto (surjective).
-
Groups and Fields: In abstract algebra, the concept of inverses is crucial in defining groups and fields. A group is a set with a binary operation that satisfies several axioms, including the existence of an inverse element for every element in the set. A field is a special type of group with additional properties.
-
Modular Arithmetic: Reciprocals exist in modular arithmetic, where numbers "wrap around" after reaching a certain modulus. However, the existence of a reciprocal depends on the greatest common divisor (GCD) between the number and the modulus. If the GCD is 1 (meaning they are relatively prime), the reciprocal exists.
Conclusion: The Significance of Understanding Reciprocals
The seemingly simple question of finding the reciprocal of -2 unveils a profound journey through the heart of mathematical principles. From the basic definition to its numerous applications in various fields, understanding reciprocals is fundamental for anyone seeking a solid grasp of mathematics and its practical implications. This exploration has highlighted the importance of reciprocals in solving equations, simplifying calculations, and understanding advanced mathematical structures. By comprehending the properties and applications of reciprocals, we build a strong foundation for further exploration of the fascinating world of mathematics. The simplicity of the answer – -1/2 – belies the depth and breadth of the underlying concepts.
Latest Posts
Latest Posts
-
Is The Pacific Ocean Colder Than The Atlantic
Apr 02, 2025
-
1 8 Of An Ounce In Grams
Apr 02, 2025
-
How Many Feet Are In 150 Inches
Apr 02, 2025
-
What Is 30 X 40 Cm In Inches
Apr 02, 2025
-
Is Toasting Bread A Physical Or Chemical Change
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Reciprocal Of -2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
