What Is The Solution Of This Linear System
Kalali
Mar 28, 2025 · 6 min read
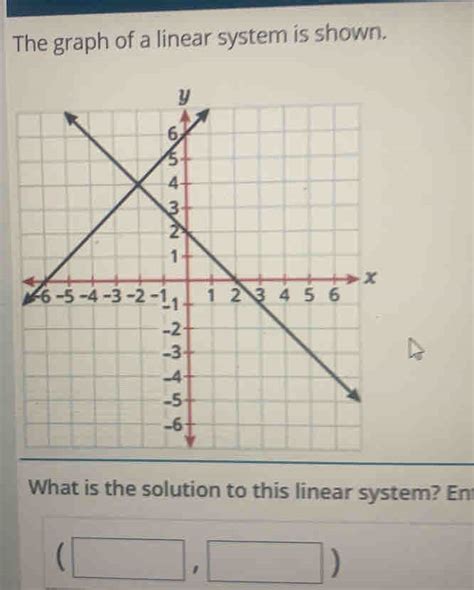
Table of Contents
What is the Solution of This Linear System? A Comprehensive Guide
Solving linear systems is a fundamental concept in mathematics and has wide-ranging applications in various fields, including engineering, computer science, economics, and physics. This article delves deep into the methods for solving linear systems, exploring different techniques and their applications. We will cover both theoretical understanding and practical examples, aiming to provide a comprehensive guide suitable for students and professionals alike.
Understanding Linear Systems
A linear system is a collection of linear equations involving the same set of variables. A simple example of a linear system with two variables is:
- 2x + y = 5
- x - y = 1
The solution to a linear system is a set of values for the variables that simultaneously satisfy all equations in the system. Geometrically, for a system of two variables, each equation represents a straight line. The solution represents the point (or points) where these lines intersect. For systems with more variables, the geometric interpretation becomes more complex, but the fundamental principle remains the same.
Methods for Solving Linear Systems
Several methods exist for solving linear systems. The choice of method often depends on the size and complexity of the system, as well as the desired level of accuracy. We will examine some of the most common techniques:
1. Substitution Method
This method involves solving one equation for one variable in terms of the others and substituting this expression into the other equations. This process continues until a single equation with one variable remains, which can then be solved. The solution for this variable is then back-substituted into the previous equations to find the values of the other variables.
Example: Let's solve the system:
- 2x + y = 5
- x - y = 1
-
Solve for one variable: From the second equation, we can easily solve for x: x = y + 1
-
Substitute: Substitute this expression for x into the first equation: 2(y + 1) + y = 5
-
Solve: Simplify and solve for y: 2y + 2 + y = 5 => 3y = 3 => y = 1
-
Back-substitute: Substitute y = 1 back into the equation x = y + 1: x = 1 + 1 => x = 2
Therefore, the solution to this system is x = 2 and y = 1.
2. Elimination Method (Gaussian Elimination)
The elimination method, also known as Gaussian elimination, is a more systematic approach, especially useful for larger systems. It involves manipulating the equations through addition, subtraction, and multiplication to eliminate variables one by one. The goal is to transform the system into an equivalent system in row echelon form or reduced row echelon form.
Steps:
-
Row Operations: Use elementary row operations (swapping rows, multiplying a row by a non-zero constant, adding a multiple of one row to another) to transform the system into row echelon form.
-
Back Substitution: Once in row echelon form, solve for the variables starting from the last equation and substituting back into the previous equations.
Example: Consider the system:
- x + 2y + z = 3
- 2x - y - z = 0
- x + y + 2z = 7
-
We can eliminate x from the second and third equations by subtracting multiples of the first equation.
-
After performing row operations, we can get the system into row echelon form. (The exact steps for row operations are lengthy and depend on the specific system, but the underlying principle is to systematically eliminate variables).
-
Then, use back substitution to find the values of x, y, and z.
This method is more efficient for larger systems and is readily implemented using computer algorithms.
3. Matrix Methods
Linear systems can be represented using matrices and vectors. This approach provides a compact and efficient way to solve systems, particularly large ones. Two primary matrix methods are:
-
Gaussian Elimination with Matrices: This is essentially the same as Gaussian elimination, but the operations are performed on the augmented matrix of the system. The augmented matrix is formed by combining the coefficient matrix and the constant vector.
-
Inverse Matrix Method: If the coefficient matrix is invertible (has a non-zero determinant), the solution can be found by multiplying the inverse of the coefficient matrix by the constant vector. This method is computationally expensive for large systems, but it offers a direct solution.
4. Cramer's Rule
Cramer's rule is a direct method for solving linear systems that uses determinants. It's generally only practical for small systems (2x2 or 3x3) because calculating determinants becomes computationally expensive for larger systems.
Formula: For a system of n linear equations with n variables, the solution for each variable xᵢ is given by:
xᵢ = det(Aᵢ) / det(A)
where A is the coefficient matrix, and Aᵢ is the matrix obtained by replacing the i-th column of A with the constant vector.
This method offers a concise formula, but its computational complexity increases rapidly with the size of the system, making it less efficient than Gaussian elimination for larger systems.
Types of Solutions
A linear system can have one of three types of solutions:
-
Unique Solution: The system has exactly one solution. This occurs when the lines (in the 2D case) intersect at a single point.
-
Infinitely Many Solutions: The system has infinitely many solutions. This happens when the equations are linearly dependent (one equation is a multiple of another). Geometrically, the lines are coincident (overlap completely).
-
No Solution: The system has no solution. This occurs when the lines (in the 2D case) are parallel and do not intersect.
Applications of Linear Systems
Linear systems have widespread applications across numerous fields:
-
Engineering: Analyzing circuits, structural analysis, and control systems.
-
Computer Science: Computer graphics, image processing, and machine learning algorithms.
-
Economics: Input-output models, linear programming, and econometrics.
-
Physics: Solving problems in mechanics, electromagnetism, and quantum mechanics.
-
Chemistry: Balancing chemical equations and analyzing chemical reactions.
Advanced Topics
For more advanced studies, the following topics are relevant:
-
Linear Algebra: Provides the theoretical foundation for understanding linear systems and their solutions.
-
Numerical Methods: Explores efficient algorithms for solving large linear systems numerically, particularly important when dealing with systems that are too large for exact analytical solutions.
-
Sparse Matrix Techniques: Specialized methods for solving linear systems where the coefficient matrix contains a high proportion of zero elements. These techniques are crucial for solving very large systems that arise in many scientific and engineering applications.
Conclusion
Solving linear systems is a fundamental skill with applications across many disciplines. This article provides a comprehensive overview of the various methods for solving these systems, ranging from simple substitution to more advanced matrix methods. The choice of method depends on the specific problem and the desired level of accuracy. Understanding the different types of solutions and their geometric interpretations is crucial for properly interpreting the results. For those wishing to delve deeper, exploring the world of linear algebra and numerical methods will unlock even more powerful tools for tackling complex problems involving linear systems.
Latest Posts
Latest Posts
-
In Many States Trailers With A Gvwr Of 1500
Jul 10, 2025
-
How Many Tablespoons Are In A Hidden Valley Ranch Packet
Jul 10, 2025
-
Which Is The Best Summary Of The Passage
Jul 10, 2025
-
How Many Quarts Of Soil In A Cubic Foot
Jul 10, 2025
-
What Is 3 4 Of A Pound
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Solution Of This Linear System . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.