What Is The Value Of 32 4
Kalali
Aug 21, 2025 · 5 min read
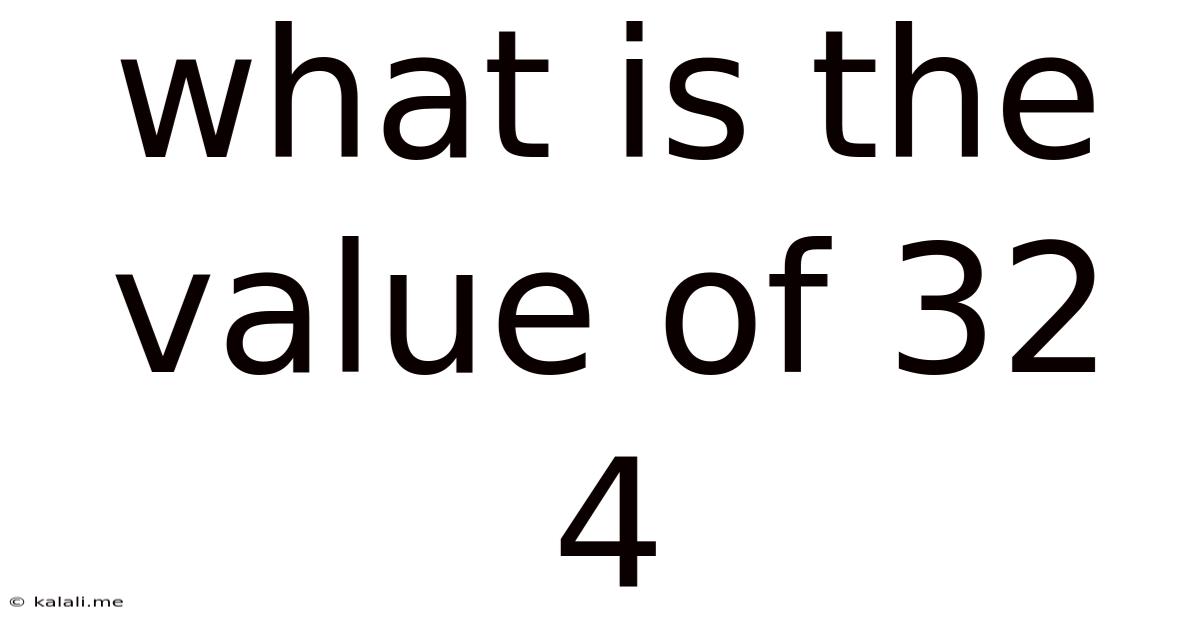
Table of Contents
Decoding the Value of "32 4": Exploring the Ambiguity and its Potential Meanings
The seemingly simple expression "32 4" presents a fascinating challenge: its value is not immediately apparent. The absence of an explicit mathematical operator (like +, -, ×, ÷) leaves the interpretation open to multiple possibilities, highlighting the importance of clear communication and the nuanced understanding of mathematical notation. This article will delve into the various ways this expression can be interpreted, exploring the underlying mathematical concepts and demonstrating the crucial role of context in determining its true value. We'll cover potential interpretations, the importance of unambiguous notation, and how this ambiguity can be avoided in various applications.
Meta Description: The expression "32 4" lacks an explicit operator, leading to multiple interpretations. This article explores the various possibilities, highlighting the importance of clear mathematical notation and contextual understanding in determining its value.
Potential Interpretations of "32 4"
The lack of an operator in "32 4" opens the door to several interpretations, each yielding a different numerical result. Let's examine the most plausible scenarios:
1. Concatenation: The simplest interpretation treats "32 4" as a concatenation of two numbers. In this case, the expression would represent the number 324. This interpretation is straightforward and relies on the assumption that the numbers are simply placed side-by-side without any implied operation.
2. Implicit Multiplication: While less common without explicit symbols, some might interpret the juxtaposition of "32" and "4" as implying multiplication. This would result in 32 × 4 = 128. This interpretation is less intuitive than concatenation but is still a valid possibility depending on the context.
3. Base Conversion: Could "32 4" represent a number in a different base? This is a less likely interpretation without further context, but it's worth considering. If we assume a base-5 system, for example, "32" would represent (3 x 5¹ + 2 x 5⁰) = 17 and "4" would remain 4. The interpretation would then depend on whether this is concatenation (174) or implicit multiplication (17 x 4 = 68). Base 6, 7, etc., would yield different values again, emphasizing the need for clear specification of the base.
4. Coordinate System: In a two-dimensional coordinate system, "32 4" could be interpreted as a coordinate pair (32, 4). This is a geometric interpretation, representing a point in a plane. The "value" here is not a single number but a location. This highlights how the interpretation of a numerical expression can entirely change based on its application.
5. Part of a Larger Expression: The expression "32 4" could be a fragment of a larger, more complex mathematical expression. Without the surrounding context, we cannot definitively determine its value or even its intended operation. For example, it could be part of a sequence: 12 2, 23 3, 32 4, where a pattern is concealed and needs to be deciphered. Without the full sequence, no specific value can be assigned.
6. Units of Measurement: This is a contextual interpretation. If "32" and "4" represent units (for example, 32 meters and 4 seconds), it becomes non-numeric and the "value" might represent a speed or distance over time, highlighting the ambiguity. In this case, the "value" depends entirely on the units involved.
The Crucial Role of Context and Unambiguous Notation
The examples above clearly illustrate the critical importance of context and unambiguous notation in mathematics. The seemingly simple expression "32 4" yields drastically different values depending on how it's interpreted. This ambiguity can lead to errors and miscommunication, particularly in fields like programming, engineering, and scientific research where precise calculations are essential.
Mathematical Notation: Mathematics relies on a system of precise notation to eliminate ambiguity. Operators (+, -, ×, ÷), parentheses ( ), and other symbols are crucial in specifying the order of operations and the intended meaning of an expression. The absence of these clarifying symbols is the root of the problem with "32 4."
Programming Languages: In programming, the lack of an explicit operator would likely result in a syntax error. Programming languages strictly enforce the use of operators to define the intended operation between numerical values. Attempting to directly evaluate "32 4" in a programming environment without an operator would likely produce an error message.
Real-World Applications: Consider the implications in a real-world setting. If "32 4" represents a measurement in a construction project or a formula in a scientific experiment, the ambiguity could have severe consequences. Incorrect interpretation can lead to errors with potentially significant repercussions.
Avoiding Ambiguity: Best Practices
To prevent similar ambiguities, several best practices should be adopted:
-
Always use explicit operators: Never rely on implied operations. Clearly state the intended operation between numbers using the appropriate symbols (+, -, ×, ÷).
-
Use parentheses to clarify order of operations: Parentheses are crucial for grouping terms and ensuring that operations are performed in the correct order, especially in complex expressions.
-
Specify units of measurement: If numbers represent measurements, always include the relevant units (e.g., meters, seconds, kilograms) to avoid confusion.
-
Define the base (if applicable): When working with numbers in bases other than 10, explicitly state the base to avoid misinterpretations.
-
Provide context: Always provide sufficient context to make the intended meaning clear. If the expression is part of a larger problem or equation, clearly present the entire equation.
-
Use descriptive variable names: In programming or scientific calculations, use descriptive variable names to improve readability and reduce the risk of misunderstanding.
Conclusion: The Importance of Precision in Mathematics and Beyond
The simple expression "32 4" serves as a potent reminder of the importance of precise mathematical notation and contextual understanding. The ambiguity it presents underscores the need for careful communication and the avoidance of implied operations. In mathematics, programming, engineering, and any field requiring precise calculations, clarity and precision are paramount. Following best practices for mathematical notation and communication can prevent errors, improve collaboration, and ensure the accuracy of results. The lesson learned from "32 4" extends far beyond simple arithmetic; it's a lesson about the critical role of clear communication in all aspects of problem-solving and knowledge transfer. The true "value" of "32 4" is not a single number, but the insight it provides into the importance of precise and unambiguous communication in quantitative analysis.
Latest Posts
Latest Posts
-
Does The Pythagorean Apply To All Triangles
Aug 21, 2025
-
Words That Start With Z And End In Q
Aug 21, 2025
-
What Is 2 Months Into An Hour
Aug 21, 2025
-
How Many Edges Does A Sphere Have
Aug 21, 2025
-
Hope All Is Well With You And Your Family
Aug 21, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of 32 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.