What Is X Squared Divided By X Squared
Kalali
Jun 30, 2025 · 5 min read
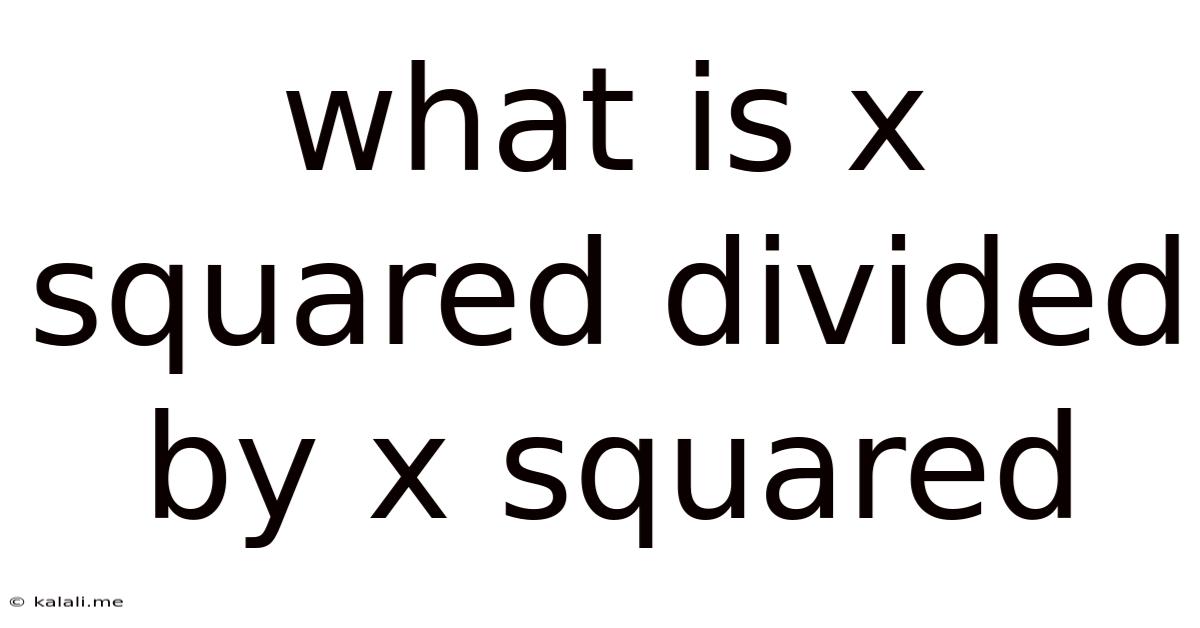
Table of Contents
What is X Squared Divided by X Squared? A Deep Dive into Algebraic Simplification
This seemingly simple question, "What is x² divided by x²?", opens a door to a fascinating exploration of algebraic simplification, the rules governing exponents, and the nuances of dealing with undefined expressions in mathematics. While the answer might seem obvious at first glance, understanding the underlying principles provides a solid foundation for tackling more complex algebraic problems. This article will explore this seemingly simple division problem, delving into its various interpretations and implications.
Meta Description: Uncover the intricacies of x²/x²! This comprehensive guide explores algebraic simplification, exponent rules, and the handling of undefined expressions, providing a solid foundation for more advanced mathematical concepts. Learn about zero, division by zero, and the importance of understanding mathematical limitations.
The Obvious Answer: 1
For most, the immediate response to x²/x² is 1. This is based on the fundamental rule of algebra: any number (except zero) divided by itself equals one. This intuition holds true for many numerical examples. For instance:
- 4² / 4² = 16 / 16 = 1
- 10² / 10² = 100 / 100 = 1
- 0.5² / 0.5² = 0.25 / 0.25 = 1
This consistent result leads us to the simplified expression:
x²/x² = 1 (where x ≠ 0)
The crucial caveat, "where x ≠ 0," is paramount. This is because division by zero is undefined in mathematics. Let's explore why this exception is so important.
The Importance of Excluding Zero: Division by Zero
The concept of division by zero is a cornerstone of mathematical understanding. It's not simply a rule to be memorized; it's a consequence of the fundamental properties of arithmetic. To illustrate, consider the definition of division:
a / b = c implies b * c = a
If we attempt to apply this to division by zero (let's say, x²/x² where x = 0), we encounter a contradiction:
0 / 0 = c implies 0 * c = 0
This equation holds true for any value of c. The result is indeterminate—it could be any number. This lack of a unique solution is why division by zero is undefined. It breaks the consistency and predictability of arithmetic operations.
Applying Exponent Rules: A Deeper Look
The simplification of x²/x² can also be approached using the rules of exponents. Specifically, the rule for dividing exponents with the same base:
xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾
Applying this rule to our problem:
x² / x² = x⁽²⁻²⁾ = x⁰
This introduces another crucial concept: the zero exponent. Any non-zero number raised to the power of zero equals one. This is a direct consequence of the exponent rule mentioned above. If we have x³/x³ we get x⁰ =1. If we extend this pattern, then it logically follows that x⁰=1. This is mathematically proven and consistent across different approaches.
Connecting the Dots: Consistency Across Methods
The two approaches—direct division and application of exponent rules—yield the same result (excluding x=0): 1. This consistency reinforces the validity of both methods and highlights the interconnectedness of various algebraic concepts. The agreement between these methods emphasizes the robustness and internal consistency of mathematical principles. It's not just a matter of getting the right answer; it's about understanding why the answer is correct and the underlying mathematical reasoning supporting it.
Beyond the Basics: Extending the Concept
Understanding x²/x² = 1 (x ≠ 0) forms a bedrock for tackling more complicated algebraic expressions. Consider these examples:
-
(3x²y) / (x²y): Here, we can simplify by canceling out common factors: (3x²y) / (x²y) = 3 (assuming x ≠ 0 and y ≠ 0). The principle of canceling common factors is directly related to the concept of x²/x² = 1.
-
(x⁴ + 2x²) / x²: This requires factoring the numerator: (x²(x² + 2)) / x² = x² + 2 (assuming x ≠ 0). Again, the simplification hinges on the understanding of dividing by x².
-
(x² - 4) / (x - 2): Factoring the numerator is essential: [(x - 2)(x + 2)] / (x - 2) = x + 2 (assuming x ≠ 2). This example showcases the significance of handling potential undefined values (division by zero).
These more advanced examples show how mastering the seemingly simple concept of x²/x² lays the groundwork for successfully navigating complex algebraic problems. The ability to confidently simplify expressions is crucial in various branches of mathematics and science.
The Importance of Mathematical Rigor
The seemingly trivial problem of x²/x² underlines the importance of mathematical rigor. It's not enough to simply obtain an answer; it's crucial to understand the conditions under which that answer is valid. The explicit exclusion of x = 0 is not just a technicality; it's a reflection of the fundamental limitations of division by zero. Ignoring this constraint can lead to incorrect conclusions and flawed reasoning.
Practical Applications: Real-World Relevance
While this might seem like a purely theoretical exercise, understanding algebraic simplification has widespread applications in various fields:
-
Physics: Many physics equations involve algebraic manipulations. The ability to simplify expressions is crucial for solving problems and interpreting results accurately.
-
Engineering: Engineers regularly use algebraic techniques for designing and analyzing systems. Proper simplification is essential for ensuring the accuracy and reliability of their designs.
-
Computer Science: Algorithms and data structures often involve manipulating mathematical expressions. Efficient simplification can significantly improve the performance of computer programs.
-
Economics: Economic models frequently use mathematical equations. The ability to simplify complex expressions allows for better understanding and interpretation of economic trends.
Conclusion: A Foundational Concept
The seemingly simple question, "What is x² divided by x²?", has led us on a journey through core algebraic principles, exponent rules, and the critical importance of considering undefined expressions. While the answer is 1 (provided x ≠ 0), the real value lies in understanding the underlying mathematical reasoning and the implications of division by zero. This foundational concept forms a cornerstone for more advanced algebraic manipulations and has far-reaching applications in various fields. Mastering this seemingly simple concept is a crucial step in building a strong mathematical foundation. Remember to always consider the limitations and exceptions inherent in mathematical operations to ensure accuracy and avoid errors. The understanding of x²/x² is not merely about the answer; it is about the journey of understanding the rules and limitations that govern mathematics.
Latest Posts
Latest Posts
-
How Long Would It Take To Walk 0 4 Miles
Jun 30, 2025
-
How Much Is 6 Oz Of Yogurt
Jun 30, 2025
-
How Many Ccs Are In A Pound
Jun 30, 2025
-
How Many Times Does 5 Go Into 2
Jun 30, 2025
-
How Many Weeks Are In 2 Months
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about What Is X Squared Divided By X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.