What Is X Squared Times X Squared
Kalali
Aug 25, 2025 · 5 min read
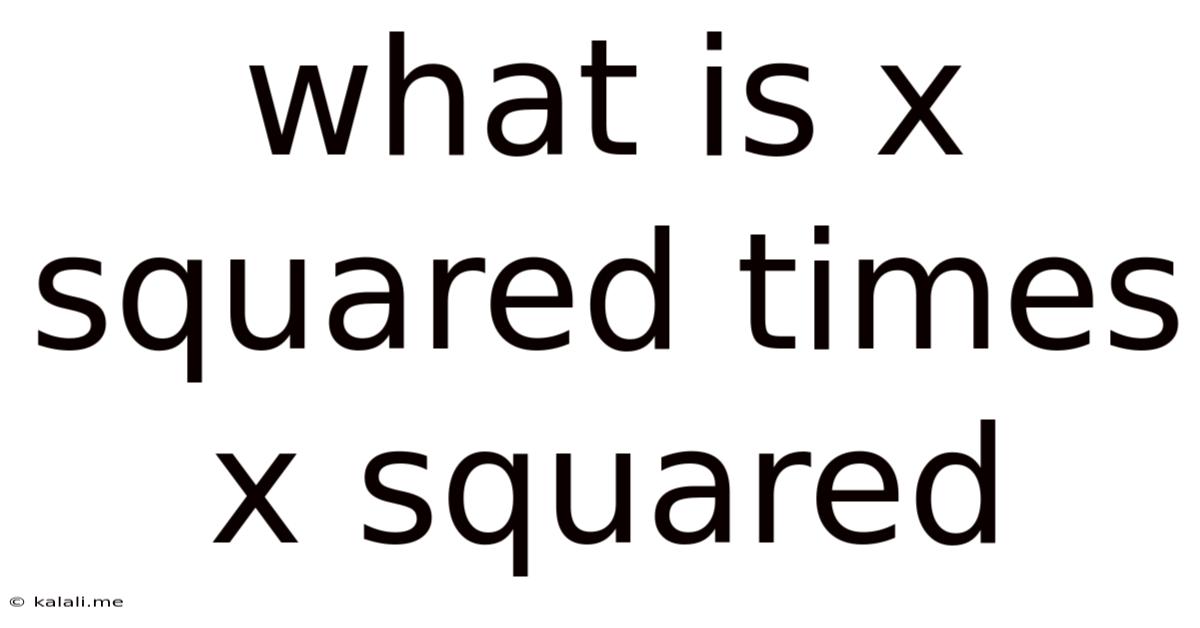
Table of Contents
What is X Squared Times X Squared? A Deep Dive into Exponents and Algebraic Simplification
This seemingly simple question, "What is x squared times x squared?", opens the door to a deeper understanding of exponents, algebraic manipulation, and the fundamental rules governing mathematical operations. While the immediate answer might seem straightforward, exploring the underlying principles provides a strong foundation for more complex algebraic problems. This article will not only answer the question but will also delve into the reasoning behind the solution, explore related concepts, and provide examples to solidify your understanding.
Meta Description: Learn how to solve x² * x² and understand the fundamental rules of exponents. This comprehensive guide explores algebraic simplification, provides step-by-step examples, and explains related mathematical concepts.
Before we tackle the core problem, let's establish some fundamental concepts related to exponents and algebraic simplification.
Understanding Exponents
An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For instance, in the expression x², the '2' is the exponent, and 'x' is the base. x² means x * x. Understanding this basic definition is crucial to solving our problem. The exponent signifies repeated multiplication, not addition. This is a common point of confusion for beginners.
The Product Rule of Exponents
The key to solving x² * x² lies in understanding the product rule of exponents. This rule states that when multiplying two terms with the same base, you can add their exponents. Mathematically, this is represented as:
xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾
This rule is the cornerstone of simplifying expressions involving exponents with the same base. It allows us to streamline complex expressions into simpler, more manageable forms.
Solving X Squared Times X Squared
Now, let's apply the product rule to solve our original problem: x² * x².
Following the product rule:
x² * x² = x⁽²⁺²⁾ = x⁴
Therefore, x squared times x squared equals x to the power of four, or x⁴.
This seemingly simple solution masks a deeper understanding of exponential properties and algebraic manipulation. Let's break down the process further.
Step-by-Step Breakdown
-
Identify the Base and Exponents: In the expression x² * x², the base is 'x', and the exponents are both '2'.
-
Apply the Product Rule: Since we are multiplying terms with the same base, we apply the product rule: xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾.
-
Add the Exponents: Adding the exponents (2 + 2), we get 4.
-
Write the Simplified Expression: The simplified expression is x⁴.
Visual Representation
To further solidify understanding, let's visualize the multiplication:
x² * x² = (x * x) * (x * x) = x * x * x * x = x⁴
This visualization clearly demonstrates that multiplying x² by itself results in four instances of 'x' multiplied together, hence x⁴.
Expanding the Concept: More Complex Examples
The principles discussed above can be extended to more complex scenarios involving multiple terms and different exponents. Let's examine a few examples:
Example 1: x³ * x⁵
Applying the product rule: x³ * x⁵ = x⁽³⁺⁵⁾ = x⁸
Example 2: 2x² * 3x⁴
Here, we multiply the coefficients (2 and 3) separately and then apply the product rule to the variables:
2x² * 3x⁴ = (2 * 3) * (x² * x⁴) = 6x⁽²⁺⁴⁾ = 6x⁶
Example 3: (x²)³
This example involves a power raised to a power. The rule for this is to multiply the exponents:
(x²)³ = x⁽²*³⁾ = x⁶
This highlights another crucial aspect of working with exponents – the power of a power rule.
Practical Applications
Understanding exponential rules is fundamental in various fields, including:
-
Physics: Calculating quantities like velocity, acceleration, and energy often involve exponential expressions.
-
Engineering: Designing structures, circuits, and systems relies heavily on mathematical modeling that frequently uses exponents.
-
Finance: Compound interest calculations are based on exponential growth.
-
Computer Science: Algorithmic complexity and data structure analysis frequently use exponential notation to describe efficiency.
-
Statistics and Probability: Many statistical distributions involve exponential functions.
Common Mistakes to Avoid
When working with exponents, it's crucial to avoid common pitfalls:
-
Confusing Addition and Multiplication: Remember that exponents represent repeated multiplication, not addition. x² + x² ≠ x⁴; instead, x² + x² = 2x².
-
Incorrect Application of the Product Rule: The product rule applies only when the bases are the same. x² * y² cannot be simplified using the product rule.
-
Forgetting the Coefficient: When multiplying terms with coefficients, remember to multiply the coefficients separately before applying the product rule to the variables.
-
Incorrect Power of a Power Rule: When raising a power to a power, remember to multiply the exponents, not add them.
Further Exploration
This article provides a solid foundation for understanding the simplification of x² * x². However, exploring more advanced concepts can deepen your mathematical skills:
-
Negative Exponents: Understanding how negative exponents work is essential for handling more complex algebraic expressions.
-
Fractional Exponents: Fractional exponents represent roots (e.g., x^(1/2) = √x).
-
Zero Exponent: Any non-zero number raised to the power of zero equals 1 (x⁰ = 1).
-
Scientific Notation: Scientific notation utilizes exponents to represent very large or very small numbers concisely.
By mastering the fundamental concepts and avoiding common mistakes, you'll be well-equipped to tackle more complex algebraic expressions involving exponents. Remember that consistent practice and a clear understanding of the rules are key to success in algebra. This seemingly simple question, "What is x squared times x squared?", serves as a gateway to a much broader understanding of mathematical principles and their real-world applications. Continuously exploring and challenging yourself with more complex problems will solidify your understanding and enhance your mathematical abilities.
Latest Posts
Latest Posts
-
What Does The Circle In The Triangle Mean
Aug 25, 2025
-
Mikes Hard Lemonade How Many To Get Drunk
Aug 25, 2025
-
Vocab Workshop Level C Unit 9 Answers
Aug 25, 2025
-
How To Write 2500 00 On A Check
Aug 25, 2025
-
Which Website Is Probably The Most Trustworthy Media Source
Aug 25, 2025
Related Post
Thank you for visiting our website which covers about What Is X Squared Times X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.