What Number Is 15 Of 60
Kalali
Mar 28, 2025 · 4 min read
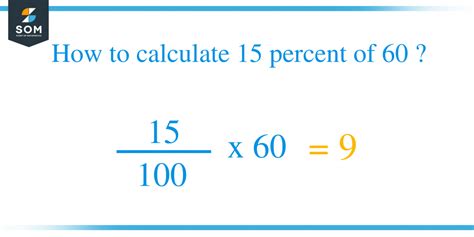
Table of Contents
What Number is 15 of 60? Understanding Fractions, Percentages, and Ratios
The question "What number is 15 of 60?" might seem simple at first glance, but it opens the door to a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. This seemingly straightforward query allows us to explore various methods for solving it and, more importantly, understand the underlying principles that govern these calculations. Let's dive in!
Understanding the Question: Different Interpretations
Before we jump into calculations, it's crucial to understand what the question actually means. It can be interpreted in several ways:
- Fraction: What fraction of 60 is 15? This asks us to express the relationship between 15 and 60 as a fraction.
- Percentage: What percentage of 60 is 15? This seeks to express the relationship as a percentage, a way of representing fractions out of 100.
- Ratio: What is the ratio of 15 to 60? This focuses on the proportional relationship between the two numbers.
While these interpretations lead to different representations, they all essentially ask the same thing: how does 15 relate to 60 in terms of proportion?
Method 1: Solving as a Fraction
The most straightforward approach is to express the relationship as a fraction. We can represent "15 of 60" as the fraction 15/60.
Simplifying the Fraction
The fraction 15/60 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of 15 and 60. The GCD is 15. Dividing both the numerator and the denominator by 15, we get:
15/60 = (15 ÷ 15) / (60 ÷ 15) = 1/4
Therefore, 15 is one-quarter of 60.
Method 2: Solving as a Percentage
To express the relationship as a percentage, we first calculate the fraction as we did above (15/60 = 1/4). Then, we convert this fraction to a percentage by multiplying by 100:
(1/4) * 100 = 25%
Therefore, 15 is 25% of 60. This means that 15 represents 25 out of every 100 parts of 60.
Method 3: Solving as a Ratio
A ratio expresses the proportional relationship between two numbers. The ratio of 15 to 60 is written as 15:60. Similar to the fraction method, we can simplify this ratio by dividing both numbers by their GCD (which is 15):
15:60 = (15 ÷ 15) : (60 ÷ 15) = 1:4
Therefore, the ratio of 15 to 60 is 1:4. This indicates that for every one part of 15, there are four parts of 60.
Real-World Applications: Understanding Proportions
Understanding fractions, percentages, and ratios is crucial in numerous real-world scenarios:
1. Shopping and Sales
Imagine a shirt originally priced at $60 is on sale for $15. Using the methods above, we can quickly determine that the discount is 25% or 1/4 of the original price.
2. Recipe Scaling
If a recipe calls for 15 grams of sugar for a batch that yields 60 cookies, and you want to make only 15 cookies, you would need to reduce the sugar amount proportionally. Using the ratio 1:4, you would use only 3.75 grams of sugar (15 grams / 4).
3. Data Analysis
In data analysis, understanding proportions is essential for interpreting data. For example, if 15 out of 60 survey respondents answered "yes" to a particular question, you could express this as 25% or a 1:3 ratio of "yes" to "no" responses.
4. Financial Calculations
Interest rates, loan repayments, and investment returns are all expressed as percentages or ratios. Understanding these concepts is crucial for making informed financial decisions.
5. Construction and Engineering
In construction and engineering, ratios and proportions are used extensively in calculating material quantities, scaling drawings, and ensuring structural integrity.
Expanding the Concept: More Complex Proportions
The example of 15 of 60 provides a foundation for understanding more complex proportional problems. Let's explore how these concepts extend:
Solving for Unknown Values
What if we reversed the problem? Let's say we know that 25% of a number is 15. How would we find the original number?
We can set up an equation: 0.25 * x = 15
Solving for x, we get: x = 15 / 0.25 = 60
This reinforces the relationship we've established.
Dealing with Larger Numbers
The principles remain the same even when dealing with larger numbers. For example, if we wanted to find what percentage 150 is of 600, we would still use the same methods:
150/600 = 1/4 = 25%
The ratio would simplify to 1:4 as well.
Conclusion: Mastering Proportions for a Stronger Foundation
Understanding the relationship between 15 and 60 – whether expressed as a fraction, percentage, or ratio – is a fundamental skill applicable across various fields. Mastering these concepts builds a strong mathematical foundation, enhancing problem-solving abilities and enabling a deeper comprehension of data and proportions in real-world situations. From simple shopping calculations to complex engineering projects, the ability to work with fractions, percentages, and ratios is an invaluable asset. The seemingly simple question, "What number is 15 of 60?", therefore, opens a window to a vast world of practical applications and mathematical understanding. Remember to always simplify your answers to their simplest forms for clarity and efficiency.
Latest Posts
Latest Posts
-
Dimension Of A Cylinder Factor Of 5
Mar 31, 2025
-
Convert 1 1 2 Oz To Cups
Mar 31, 2025
-
How Many Ounces Is A Quarter Of A Pound
Mar 31, 2025
-
The Right Shoulder Is And To The Umbilical Region
Mar 31, 2025
-
How Many Feet Is 190 In
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Number Is 15 Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
