What Number Is 24 Percent Of 75
Kalali
Jul 27, 2025 · 5 min read
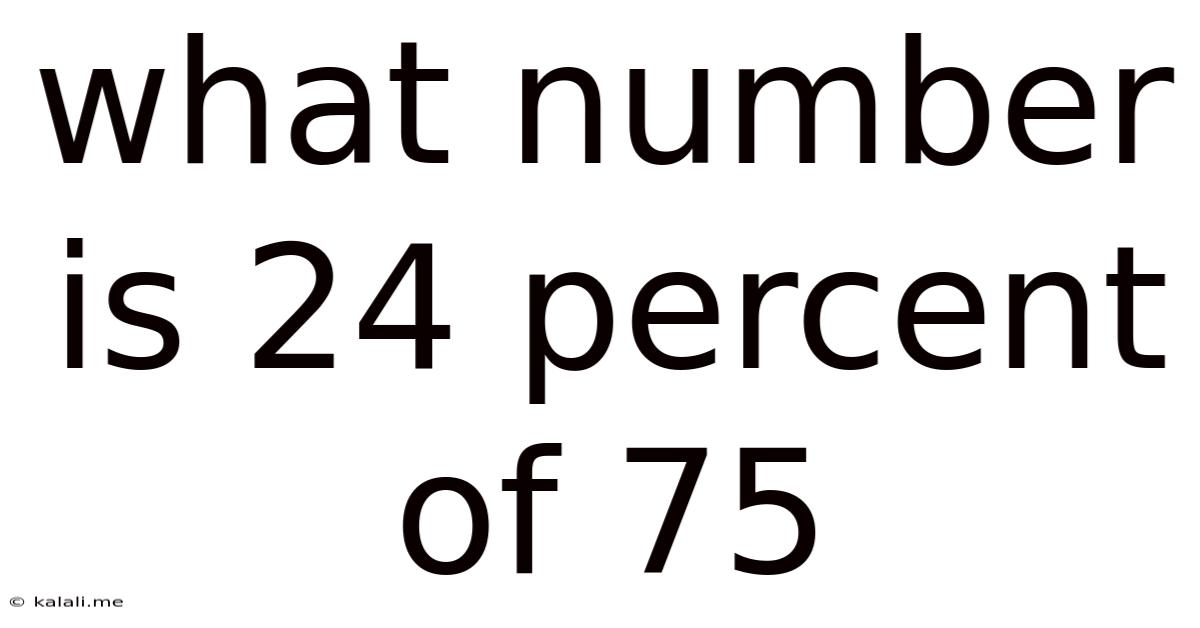
Table of Contents
What Number is 24 Percent of 75? A Comprehensive Guide to Percentage Calculations
Finding out what number represents 24 percent of 75 might seem like a simple arithmetic problem, but understanding the underlying concepts and different methods for solving it is crucial for various applications, from everyday budgeting and shopping to more complex financial analyses and scientific calculations. This comprehensive guide will delve into various approaches to solving this problem, explaining each method thoroughly and providing practical examples. We'll also explore the broader context of percentage calculations and their importance.
Meta Description: Learn how to calculate 24% of 75 using multiple methods, including the basic formula, fractions, and proportions. This guide provides a comprehensive understanding of percentage calculations and their real-world applications.
The answer to the question, "What number is 24 percent of 75?" is 18. However, simply providing the answer doesn't convey the understanding necessary to tackle similar problems independently. Let's explore the different ways to arrive at this solution and gain a deeper appreciation for percentage calculations.
Method 1: The Basic Percentage Formula
The most fundamental approach involves using the basic percentage formula:
Part = Percentage × Whole
In this case:
- Part: This is the unknown value we want to find – the number that represents 24% of 75.
- Percentage: This is 24%, which needs to be converted to a decimal by dividing by 100 (24/100 = 0.24).
- Whole: This is the total value, which is 75.
Substituting the values into the formula:
Part = 0.24 × 75 = 18
Therefore, 24% of 75 is 18.
This method is straightforward and easily adaptable to various percentage problems. Simply change the percentage and whole value to solve for different scenarios. For example, finding 15% of 200 would involve substituting 0.15 for the percentage and 200 for the whole.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 24% can be written as 24/100. The problem then becomes:
(24/100) × 75
This can be simplified:
(24 × 75) / 100 = 1800 / 100 = 18
This method highlights the relationship between fractions and percentages, emphasizing that percentages are simply fractions with a denominator of 100. This approach is particularly useful when dealing with percentages that can be easily simplified into smaller fractions. For instance, 50% is easily recognized as 1/2, making calculations more intuitive.
Method 3: Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion:
24/100 = x/75
Here:
- 24 represents the percentage.
- 100 represents the total percentage (100%).
- x represents the unknown part we are trying to find.
- 75 represents the whole value.
To solve for x, we cross-multiply:
24 × 75 = 100 × x
1800 = 100x
x = 1800 / 100 = 18
This method is particularly helpful when visualizing the relationship between the parts and the whole. It provides a clear picture of how the percentage relates to the total value. It's a powerful technique that can be adapted to solve complex percentage problems involving multiple unknowns.
Method 4: Using a Calculator
While the above methods highlight the underlying mathematical principles, using a calculator simplifies the process, especially for more complex percentages or larger numbers. Most calculators have a percentage function (%) that directly calculates the percentage of a number. Simply enter 75, press the multiplication key, enter 24, press the percentage key, and the calculator will display the result: 18.
This is a convenient method for quick calculations, especially in situations where speed is essential.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is fundamental in numerous real-world situations:
-
Financial Calculations: Calculating interest on loans, savings accounts, and investments relies heavily on percentage calculations. Understanding interest rates, annual percentage yields (APYs), and compound interest requires a firm grasp of percentages.
-
Sales and Discounts: Retailers frequently offer discounts expressed as percentages. Calculating the final price after a discount involves subtracting the percentage of the discount from the original price. For example, a 20% discount on a $50 item would reduce the price by $10 (20% of $50), resulting in a final price of $40.
-
Tax Calculations: Sales tax, income tax, and other taxes are commonly expressed as percentages. Calculating the total amount payable, including taxes, necessitates the application of percentage calculations.
-
Data Analysis: Percentages are essential for interpreting data and presenting statistical information effectively. For instance, market share, survey results, and growth rates are often expressed as percentages to provide a clear and concise picture of trends and changes.
-
Scientific Calculations: Percentage calculations are used in many scientific fields, including chemistry, biology, and physics. For instance, concentration of solutions, efficiency of processes, and statistical analyses often utilize percentage calculations.
-
Everyday Budgeting: Budgeting and managing personal finances often require estimating percentages for allocating funds to different categories (e.g., rent, food, transportation).
-
Tip Calculations: Calculating tips in restaurants typically involves calculating a percentage of the total bill.
Advanced Percentage Problems and Considerations
While the problem "What number is 24 percent of 75?" is relatively simple, the principles can be extended to more complex situations. For example:
-
Finding the percentage: If you know the part and the whole, you can calculate the percentage using the formula: Percentage = (Part/Whole) × 100
-
Finding the whole: If you know the part and the percentage, you can find the whole using the formula: Whole = Part / (Percentage/100)
-
Percentage increase/decrease: Calculating percentage change involves finding the difference between two values and expressing it as a percentage of the original value. Percentage increase = [(New Value - Old Value) / Old Value] × 100, and percentage decrease is calculated similarly.
-
Compound Interest: Compound interest calculations involve repeatedly applying interest to the principal amount plus accumulated interest, leading to exponential growth.
Mastering these fundamental percentage calculations is essential for tackling these more advanced problems.
Conclusion
Understanding how to calculate 24% of 75, and more generally, how to work with percentages, is a crucial skill applicable across a vast range of situations. The different methods discussed in this article – using the basic formula, fractions, proportions, and calculators – provide flexibility and a deeper understanding of the underlying mathematical principles. By mastering these techniques, you will be better equipped to handle everyday financial calculations, data analysis, and more complex mathematical problems involving percentages. Remember, the ability to confidently calculate percentages is not only valuable for academic pursuits but also empowers you to make informed decisions in various aspects of your life.
Latest Posts
Latest Posts
-
How Many Oz Are In 3 Lbs
Jul 27, 2025
-
Did You Hear About The Worksheet Answers
Jul 27, 2025
-
When A Shotgun Fires A Sequence Of Events Takes Place
Jul 27, 2025
-
Least Common Multiple Of 12 And 27
Jul 27, 2025
-
Is Wiz Khalifa And Snoop Dogg Related
Jul 27, 2025
Related Post
Thank you for visiting our website which covers about What Number Is 24 Percent Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.