What Percent Is 1 Out Of 7
Kalali
Apr 15, 2025 · 5 min read
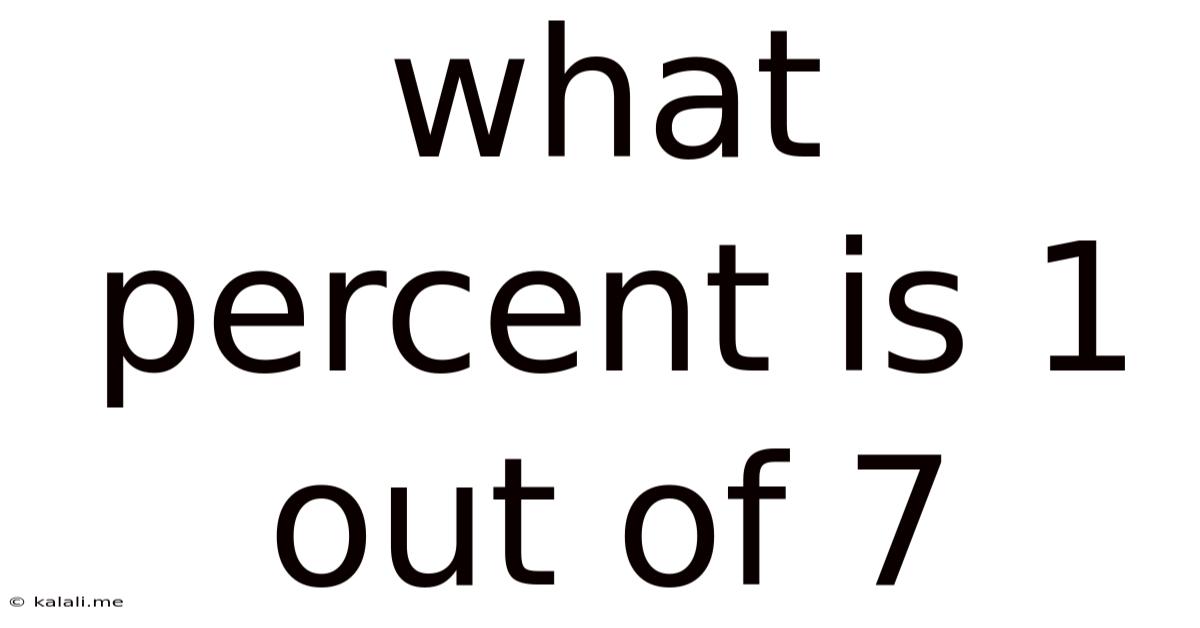
Table of Contents
What Percent is 1 out of 7? A Comprehensive Guide to Percentage Calculations
What percent is 1 out of 7? This seemingly simple question opens the door to a deeper understanding of percentages, their applications, and how to confidently calculate them. This comprehensive guide will not only answer this specific question but also equip you with the knowledge and skills to tackle similar percentage problems with ease. We'll explore different methods of calculation, delve into the underlying concepts, and provide real-world examples to solidify your understanding.
Understanding Percentages:
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "per hundred." When we say "x percent," we're indicating x parts out of 100. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental concept is crucial for all percentage calculations.
Method 1: Direct Conversion to Percentage
The most straightforward method to determine what percent 1 out of 7 represents involves converting the fraction 1/7 into a percentage. This is done in two steps:
-
Convert the fraction to a decimal: Divide the numerator (1) by the denominator (7). 1 ÷ 7 ≈ 0.142857.
-
Convert the decimal to a percentage: Multiply the decimal by 100. 0.142857 × 100 ≈ 14.29%.
Therefore, 1 out of 7 is approximately 14.29%.
Method 2: Using Proportions
Another effective approach involves setting up a proportion. We know that 1 out of 7 is equivalent to 'x' out of 100 (where 'x' represents the percentage). This can be written as:
1/7 = x/100
To solve for 'x', we cross-multiply:
7x = 100
x = 100/7
x ≈ 14.29
Hence, using proportions, we again arrive at the answer: 1 out of 7 is approximately 14.29%.
Method 3: Applying the Percentage Formula
The percentage formula provides a more generalized approach to solving percentage problems. The formula is:
Percentage = (Part / Whole) × 100
In our case:
- Part = 1
- Whole = 7
Substituting these values into the formula:
Percentage = (1 / 7) × 100 ≈ 14.29%
This method reinforces the fundamental concept of percentages and offers a systematic way to calculate them.
Rounding and Accuracy:
It's important to note that the answer, 14.29%, is a rounded value. The decimal representation of 1/7 is a repeating decimal (0.142857142857...). The level of rounding depends on the desired accuracy. For most practical purposes, rounding to two decimal places (14.29%) is sufficient. However, for scientific or engineering applications, more decimal places might be necessary.
Real-World Applications:
Understanding percentages is essential in many real-world scenarios:
-
Sales and Discounts: Calculating discounts, sale prices, and markups. For example, if a store offers a 14.29% discount on an item, you can easily calculate the discounted price.
-
Finance and Investing: Determining interest rates, returns on investments, and calculating loan repayments. Understanding percentage changes in investment values is crucial for financial planning.
-
Statistics and Data Analysis: Representing data as percentages helps in comparing and visualizing different proportions within a dataset. For instance, if 1 out of 7 people surveyed prefer a particular brand, that represents approximately 14.29% market share.
-
Science and Engineering: Percentages are commonly used in expressing concentrations, efficiencies, and error margins in scientific and engineering calculations.
-
Everyday Life: From calculating tips in restaurants to understanding the nutritional content of food, percentages are ubiquitous in our daily lives.
Beyond 1 out of 7: Expanding Your Understanding
The principles discussed above can be easily extended to calculate percentages for other fractions. For example:
- What percent is 2 out of 7? (2/7) × 100 ≈ 28.57%
- What percent is 3 out of 7? (3/7) × 100 ≈ 42.86%
- What percent is 5 out of 7? (5/7) × 100 ≈ 71.43%
By applying the same methods—direct conversion, proportions, or the percentage formula—you can confidently calculate the percentage for any fraction.
Understanding the Relationship Between Fractions, Decimals, and Percentages:
It's crucial to grasp the interconnectedness of fractions, decimals, and percentages. They are simply different ways of expressing the same numerical value:
- Fraction: Represents a part of a whole as a ratio of two numbers (numerator/denominator).
- Decimal: Represents a part of a whole using base-10 notation (e.g., 0.1429).
- Percentage: Represents a part of a whole as a fraction of 100 (e.g., 14.29%).
The ability to seamlessly convert between these forms is vital for proficient mathematical calculations.
Advanced Percentage Calculations:
While the focus here has been on basic percentage calculations, there are more complex scenarios involving percentage increase/decrease, compound interest, and more. These advanced topics build upon the foundational knowledge of basic percentage calculations. Understanding the fundamentals is the crucial first step in mastering these more advanced concepts.
Practice Makes Perfect:
The best way to solidify your understanding of percentage calculations is through practice. Try working through various examples, varying the fractions and applying the different methods we've explored. You'll soon find yourself confidently calculating percentages in any situation.
Conclusion:
In conclusion, 1 out of 7 is approximately 14.29%. This article has provided a thorough explanation of how to calculate percentages, incorporating various methods and real-world examples to ensure a comprehensive understanding. By mastering these techniques, you'll be well-equipped to tackle any percentage problem you encounter, from simple calculations to more complex scenarios. Remember the core relationship between fractions, decimals, and percentages – the ability to move fluidly between these representations is key to achieving accuracy and confidence in your calculations. With consistent practice, you will become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
How Does The Monster Try To Gain Control Of Victor
Jul 14, 2025
-
Why Did The Cow Want A Divorce
Jul 14, 2025
-
Lowest Common Denominator For 3 4 5
Jul 14, 2025
-
Can You Be A Professor With A Masters
Jul 14, 2025
-
How Many Bottles Of Water Is 1 Liter
Jul 14, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 1 Out Of 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.