What Percent Is 10 Out Of 12
Kalali
Mar 08, 2025 · 5 min read
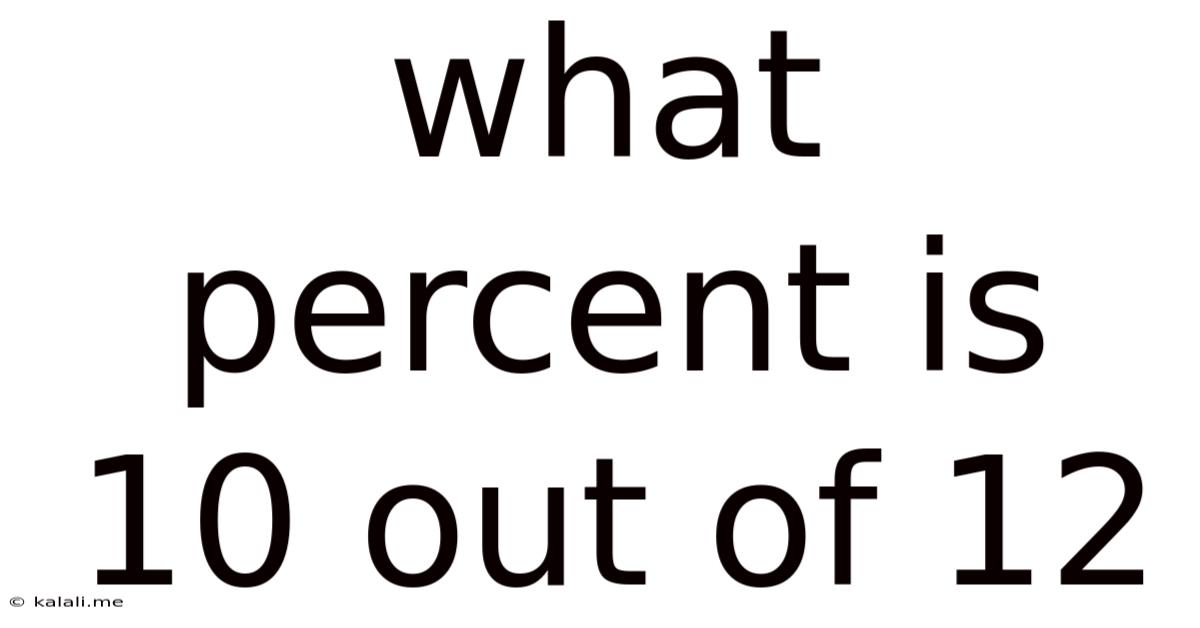
Table of Contents
What Percent is 10 Out of 12? A Comprehensive Guide to Percentage Calculations
Determining what percentage 10 out of 12 represents might seem like a simple arithmetic problem. However, understanding the underlying principles of percentage calculations is crucial for various applications, from everyday budgeting and shopping to complex statistical analysis and scientific research. This comprehensive guide will not only answer the initial question but also equip you with the knowledge and skills to tackle similar percentage problems with confidence.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" (from the Latin per centum). So, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental concept is key to performing percentage calculations.
Calculating the Percentage: 10 Out of 12
To find out what percentage 10 out of 12 represents, we need to follow these simple steps:
Step 1: Express the values as a fraction.
The problem "10 out of 12" can be written as the fraction 10/12.
Step 2: Convert the fraction to a decimal.
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
10 ÷ 12 = 0.8333... (The 3's repeat infinitely)
Step 3: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%):
0.8333... × 100 = 83.33...%
Therefore, 10 out of 12 is approximately 83.33%.
Rounding and Precision
In many real-world applications, you'll need to round your answer to a certain number of decimal places. The level of precision depends on the context. For example:
- For general purposes: Rounding to one decimal place (83.3%) is usually sufficient.
- For financial calculations: You might need to round to two or more decimal places for accuracy (83.33%).
- For scientific calculations: The required precision will depend on the specific application and might involve more significant figures.
Remember to always state the level of precision used in your calculations to avoid ambiguity.
Alternative Calculation Methods
While the above method is straightforward, there are other ways to calculate percentages. These alternative approaches can be useful in different situations and might provide a deeper understanding of the underlying concepts.
Using Proportions
A proportion is an equation that states that two ratios are equal. We can set up a proportion to solve for the percentage:
x/100 = 10/12
To solve for x (the percentage), we cross-multiply:
12x = 1000
x = 1000/12 = 83.333...%
This method clearly demonstrates the relationship between the fraction and the percentage.
Using a Calculator
Most calculators have a percentage function (%) that simplifies the process. You can simply input 10 ÷ 12 and then press the "%" button to get the answer directly. This is especially useful for quick calculations.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in many areas of life:
Finance and Budgeting:
- Calculating interest rates: Understanding interest rates is crucial for managing loans, investments, and savings accounts.
- Determining discounts: Calculating discounts helps you save money while shopping.
- Analyzing financial statements: Percentages are used extensively in analyzing financial performance, including profit margins, return on investment (ROI), and expense ratios.
- Tax calculations: Taxes are often expressed as a percentage of income or the value of goods and services.
Science and Statistics:
- Data analysis: Percentages are frequently used to represent proportions and probabilities in statistical analysis.
- Scientific measurements: Percentages are used to express changes in quantities, such as percentage increase or decrease in experimental results.
Everyday Life:
- Calculating tips: Calculating tips in restaurants involves determining a percentage of the total bill.
- Understanding sales tax: Sales tax is usually expressed as a percentage of the purchase price.
- Comparing prices: Percentages help compare prices and find the best deals.
Beyond the Basics: Advanced Percentage Problems
While calculating "what percent is 10 out of 12" is a fundamental percentage problem, there are more complex scenarios to consider. Let's explore some advanced applications:
Percentage Increase and Decrease:
Determining the percentage increase or decrease between two values requires a slightly different approach. The formula for percentage change is:
[(New Value - Old Value) / Old Value] × 100%
For instance, if a product's price increases from $10 to $12, the percentage increase is:
[(12 - 10) / 10] × 100% = 20%
Similarly, if the price decreases from $12 to $10, the percentage decrease is:
[(10 - 12) / 12] × 100% = -16.67%
Finding the Original Value:
Sometimes, you know the percentage and the final value, but you need to find the original value. This requires working backward using the percentage formula. For example, if a discounted item costs $10 after a 20% discount, the original price can be calculated as follows:
Let x be the original price.
x - 0.20x = $10
0.80x = $10
x = $10 / 0.80 = $12.50
The original price was $12.50.
Compound Percentages:
Compound percentages involve applying a percentage change repeatedly. This is commonly encountered in compound interest calculations, where interest earned is added to the principal amount, and subsequent interest is calculated on the increased amount. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding compound percentages is crucial for long-term financial planning.
Conclusion: Mastering Percentage Calculations
Calculating what percent 10 out of 12 represents—approximately 83.33%—is a fundamental skill applicable across numerous fields. This guide has not only answered the initial question but also explored various methods for calculating percentages, highlighting their importance in diverse contexts. By understanding the principles of percentage calculations and practicing different approaches, you can develop a strong foundation in this essential mathematical concept, empowering you to tackle more complex problems and make informed decisions in both personal and professional life. Remember to always consider the level of precision needed for your specific application and to choose the calculation method best suited for your needs. With consistent practice, you’ll master percentage calculations and confidently apply them to numerous situations.
Latest Posts
Latest Posts
-
How Many Grams In A Teaspoon Of Cinnamon
Jul 18, 2025
-
How Long To Heat Water In Microwave
Jul 18, 2025
-
40 Oz Of Water Is How Many Cups
Jul 18, 2025
-
How Many Eighths In A Quarter Pound
Jul 18, 2025
-
Can The Sine Of An Angle Ever Equal 2
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 10 Out Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.