What Percent Is 12 Of 16
Kalali
Apr 22, 2025 · 5 min read
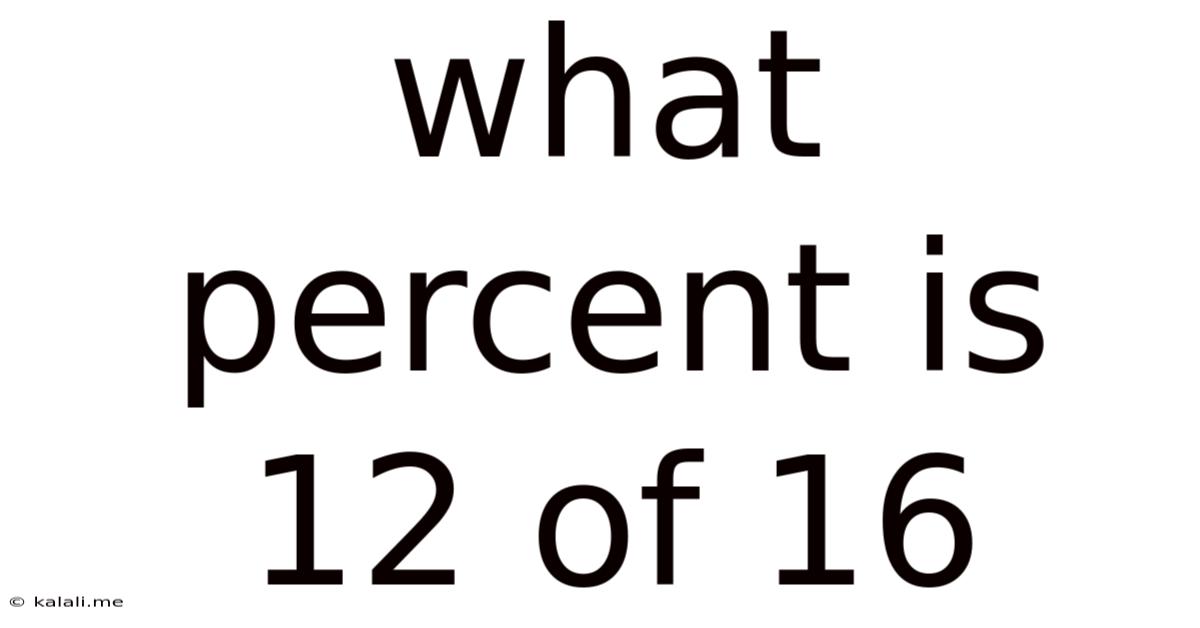
Table of Contents
What Percent is 12 of 16? A Deep Dive into Percentage Calculations and Applications
What percent is 12 of 16? This seemingly simple question opens the door to a world of percentage calculations, their applications in various fields, and the underlying mathematical principles. This comprehensive guide will not only answer the initial question but also explore the broader context of percentage calculations, providing you with a thorough understanding of the concept and its practical uses. We'll delve into different methods for calculating percentages, examine common scenarios where percentages are applied, and touch upon the importance of accurate percentage calculations in everyday life and professional settings.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" (from the Latin "per centum"). Percentages are used to represent proportions or ratios, making it easier to compare different quantities or values. They're ubiquitous in various aspects of life, from calculating discounts and taxes to understanding statistics and financial data.
The fundamental formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
Calculating "What Percent is 12 of 16?"
Now, let's tackle the initial question: What percent is 12 of 16? Applying the formula above:
(12 / 16) x 100% = 75%
Therefore, 12 is 75% of 16.
Alternative Methods for Percentage Calculation
While the basic formula is straightforward, there are alternative approaches to calculate percentages, depending on the context and the complexity of the problem. Let's explore some common methods:
-
Using Proportions: This method is especially useful when dealing with more complex percentage problems. For example, we can set up a proportion:
12/16 = x/100
Cross-multiplying, we get:
16x = 1200
Solving for x:
x = 1200 / 16 = 75
Therefore, x = 75%, confirming our earlier result.
-
Using Decimal Conversion: Convert the fraction to a decimal by dividing the part by the whole (12/16 = 0.75). Then, multiply the decimal by 100% to obtain the percentage (0.75 x 100% = 75%). This method is often faster and more convenient for simple calculations.
-
Using a Calculator: Most calculators have a percentage function that simplifies the calculation process. Simply enter 12 ÷ 16 × 100 and press the "=" button.
Practical Applications of Percentage Calculations
The ability to accurately calculate percentages is crucial in various real-world scenarios:
-
Finance: Percentages are fundamental in finance, used for calculating interest rates, loan payments, returns on investment (ROI), and understanding financial statements. For instance, understanding compound interest requires a solid grasp of percentage calculations.
-
Retail and Sales: Discounts, sales tax, markups, and profit margins are all expressed as percentages. Calculating the final price of an item after a discount or determining the profit percentage on a sale involves percentage calculations.
-
Statistics: Percentages are used extensively in statistical analysis to represent proportions, frequencies, and probabilities. Understanding statistical data often requires interpreting percentages and ratios.
-
Science and Engineering: Percentage error, percentage yield, and percentage change are important concepts in scientific experiments and engineering calculations. Accurate percentage calculations are crucial for data analysis and drawing meaningful conclusions.
-
Everyday Life: We encounter percentages daily, from calculating tips in restaurants to understanding nutrition labels on food products. Understanding percentages empowers us to make informed decisions in various aspects of our daily lives.
Common Percentage Problems and Solutions
Let's examine some common percentage problems and their solutions to reinforce the concepts discussed:
-
Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] x 100%
-
Finding a Percentage of a Number: This involves calculating a specific percentage of a given number. For example, finding 20% of 50 involves multiplying 50 by 0.20 (20/100).
-
Finding the Original Value after a Percentage Change: This requires working backward from the final value after a percentage increase or decrease. This often involves using algebraic equations.
-
Calculating Percentage Composition: In chemistry and other fields, percentage composition refers to the percentage of each element in a compound or the percentage of each component in a mixture.
Avoiding Common Mistakes in Percentage Calculations
While seemingly simple, percentage calculations can be prone to errors if not approached carefully. Here are some common mistakes to avoid:
-
Confusing Part and Whole: Ensure you correctly identify the part and the whole in the calculation.
-
Incorrect Order of Operations: Follow the correct order of operations (PEMDAS/BODMAS) to avoid arithmetic errors.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple calculations involving percentages. Round off only at the final stage of the calculation.
-
Using Incorrect Formulas: Always double-check that you are using the correct formula for the specific percentage problem.
-
Misinterpreting Percentage Changes: Percentage increases and decreases are not additive. A 10% increase followed by a 10% decrease does not result in the original value.
Advanced Percentage Concepts
For more advanced applications, understanding concepts like compound interest, exponential growth, and decay is crucial. These concepts build upon the foundation of basic percentage calculations and are essential for understanding various financial and scientific phenomena.
Conclusion: The Importance of Mastering Percentage Calculations
Understanding and accurately calculating percentages is a vital skill in numerous aspects of life, from personal finance and shopping to professional fields like science, engineering, and business. Mastering percentage calculations empowers you to make informed decisions, analyze data effectively, and solve various real-world problems. By understanding the fundamental formula, alternative calculation methods, and common applications, you can confidently tackle any percentage-related challenge. The initial question, "What percent is 12 of 16?", serves as a gateway to a much broader understanding of this essential mathematical concept. Remember to practice regularly to solidify your understanding and improve your accuracy.
Latest Posts
Latest Posts
-
What Percent Is 80 Of 120
Apr 22, 2025
-
Cuanto Es 30 Ml En Onzas
Apr 22, 2025
-
Does A Screw Increase Or Decrease Force
Apr 22, 2025
-
How Long Is 47 Inches In Feet
Apr 22, 2025
-
What Is 75 Inches In Cm
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 12 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.