What Percent Is 12 Of 30
Kalali
Apr 11, 2025 · 5 min read
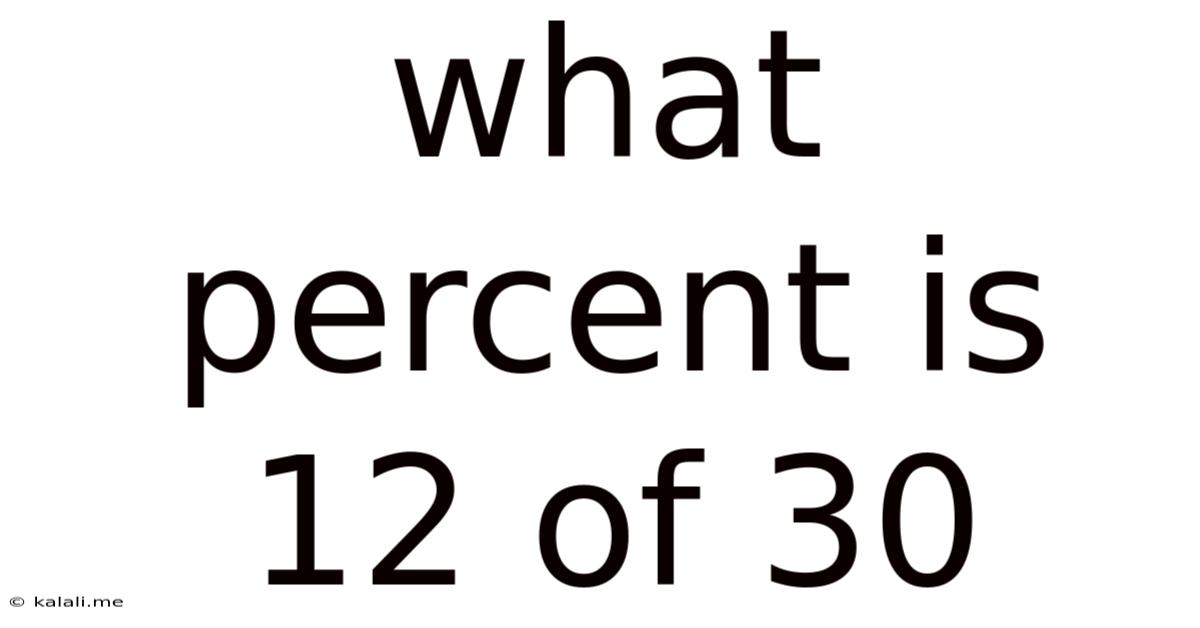
Table of Contents
What Percent is 12 of 30? A Deep Dive into Percentage Calculations
This seemingly simple question – "What percent is 12 of 30?" – opens the door to a surprisingly rich understanding of percentages, their applications, and how to solve percentage problems efficiently. This article will not only answer the question directly but also explore the underlying mathematical concepts, different calculation methods, and real-world examples to solidify your grasp of percentages. Understanding percentages is crucial in various fields, from finance and budgeting to data analysis and everyday decision-making.
Meta Description: Learn how to calculate percentages easily! This comprehensive guide answers "What percent is 12 of 30?" and explains various methods, real-world applications, and crucial percentage concepts. Master percentage calculations today!
The Direct Answer and the Formula
The direct answer to "What percent is 12 of 30?" is 40%. This is calculated using the fundamental percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
(12 / 30) * 100% = 0.4 * 100% = 40%
Understanding the Components
Let's break down the components of this formula:
- Part: This represents the specific portion you're interested in expressing as a percentage. In our example, the part is 12.
- Whole: This is the total amount or the base value to which the part belongs. In our example, the whole is 30.
- Percentage: This is the final result, expressing the part as a fraction of the whole, represented as a percentage (%).
Alternative Calculation Methods
While the formula above is the most direct approach, several other methods can be used to calculate percentages, each with its own advantages depending on the context and the numbers involved.
Method 2: Using Decimal Equivalents
We can convert the fraction (12/30) to its decimal equivalent first, then multiply by 100%:
12/30 = 0.4
0.4 * 100% = 40%
Method 3: Simplifying the Fraction
Before performing the calculation, simplifying the fraction can make the arithmetic easier:
12/30 simplifies to 2/5
(2/5) * 100% = (2 * 20%) = 40%
Method 4: Proportion Method
This method uses proportions to solve the problem:
We set up a proportion: 12/30 = x/100 where 'x' represents the percentage.
Cross-multiplying, we get: 30x = 1200
Solving for x: x = 1200 / 30 = 40
Therefore, x = 40%, meaning 12 is 40% of 30.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in our daily lives and across various professional fields. Here are some examples:
-
Finance and Budgeting: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentages. For instance, understanding that a 10% discount on a $100 item saves you $10 is a fundamental percentage application. Calculating your monthly budget, where you allocate a certain percentage to different categories like rent, food, and entertainment, is also a critical skill. Similarly, tracking your savings progress as a percentage of your financial goals helps gauge your progress.
-
Sales and Marketing: Sales representatives frequently use percentages to track their progress against sales targets. Marketing campaigns often measure their success using metrics like conversion rates (percentage of website visitors who make a purchase), click-through rates (percentage of recipients who click on a link in an email), and customer acquisition cost (percentage of marketing spend on new customers).
-
Data Analysis and Statistics: Percentages are essential for interpreting data. For example, understanding the percentage change in sales over time or the percentage of respondents who agree with a particular statement in a survey is crucial for drawing meaningful conclusions. Analyzing demographic data or consumer behavior often involves working with percentages of the total population or market.
-
Education: Grade percentages, test scores, and scholarship percentages are frequent examples in educational settings. Understanding your performance on a test relative to the total points possible often depends on calculating percentages.
-
Healthcare: Healthcare professionals frequently use percentages to represent the effectiveness of treatments, the risk factors associated with certain conditions, and various physiological measurements. For example, a doctor might mention a patient's blood oxygen saturation as a percentage.
-
Everyday Life: Calculating tips at restaurants, understanding sales tax, determining the percentage of ingredients in recipes, and many other situations require basic percentage calculations.
Advanced Percentage Problems and Concepts
While the example of 12 out of 30 is straightforward, percentage problems can get more complex. Let's explore some:
-
Finding the Whole when the Percentage and Part are Known: For example, if 20% of a number is 10, how large is the number? This requires reversing the formula: (Part / Percentage) * 100 = Whole. In this case, (10 / 20) * 100 = 50.
-
Finding the Percentage Increase or Decrease: Calculating the percentage change between two values requires knowing the initial value and the final value. The formula is: [(Final Value - Initial Value) / Initial Value] * 100%. This is commonly used in finance to track investment growth or economic indicators.
-
Compound Interest: This involves calculating interest not only on the principal amount but also on the accumulated interest. This necessitates multiple percentage calculations.
-
Percentage Points vs. Percentages: It is crucial to distinguish between these two. A change from 10% to 20% is a 10 percentage point increase, but a 100% increase.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The key to mastering percentages is consistent practice. Work through various examples, including those with different levels of complexity.
-
Understand the Concepts: Don't just memorize the formulas; understand the underlying principles of percentages and fractions.
-
Use Different Methods: Experiment with different calculation methods to find the one that best suits you and the problem you're facing.
-
Use Technology: Calculators and spreadsheet software can help expedite the calculations, freeing you up to focus on understanding the results.
Conclusion
The seemingly simple query, "What percent is 12 of 30?", leads us down a path of understanding percentage calculations, their widespread applications, and the various methods for solving percentage-related problems. Mastering percentages is a valuable skill with relevance across various fields and everyday life. Through consistent practice and understanding of fundamental concepts, you can confidently tackle percentage calculations of any complexity. Remember the formula, explore different approaches, and apply your knowledge in real-world scenarios to solidify your understanding and build your confidence in this crucial mathematical skill.
Latest Posts
Latest Posts
-
How Many Cups In 64 Ounces Of Water
Apr 18, 2025
-
What Percentage Is 15 Out Of 20
Apr 18, 2025
-
How Many Litres In A 5 Gallon Bucket
Apr 18, 2025
-
Does Gold Set Off A Metal Detector
Apr 18, 2025
-
Cuanto Son 8 Onzas De Agua
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 12 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.