What Percent Is 12 Of 40
Kalali
Apr 24, 2025 · 5 min read
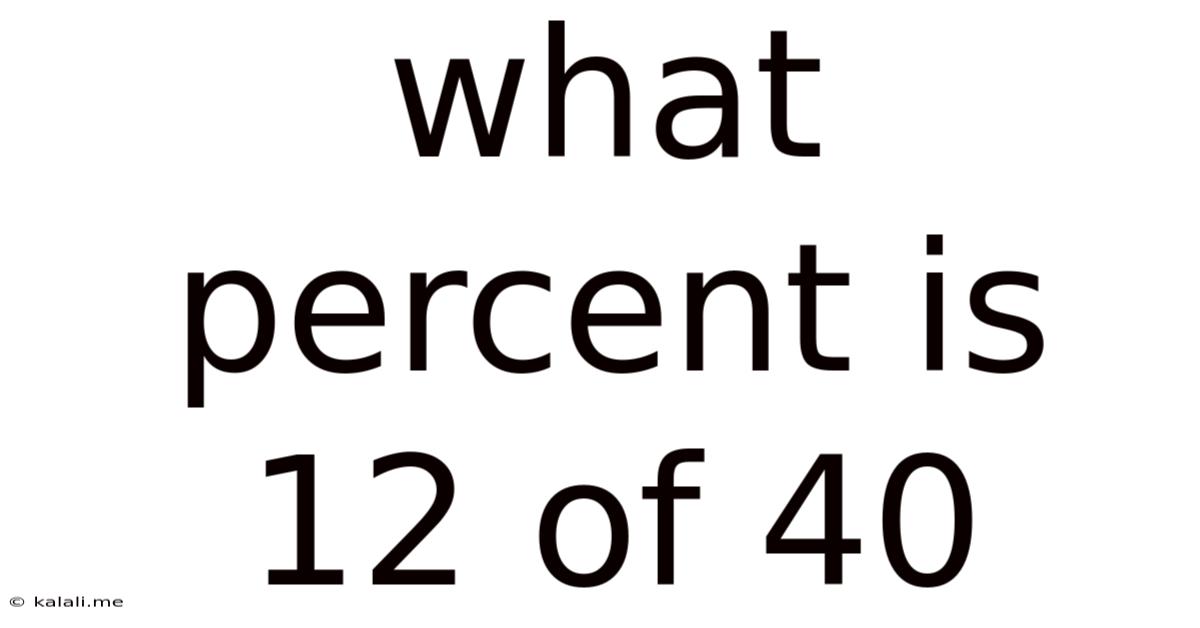
Table of Contents
What Percent is 12 of 40? A Deep Dive into Percentage Calculations and Real-World Applications
This seemingly simple question, "What percent is 12 of 40?", opens the door to a world of percentage calculations and their widespread applications in everyday life. Understanding percentages is crucial for various tasks, from calculating discounts and sales tax to comprehending financial statements and analyzing statistical data. This article will not only answer the initial question but will also delve into the methods of calculating percentages, exploring different approaches and illustrating their practical use with numerous examples.
Meta Description: Discover how to calculate percentages, specifically determining what percent 12 is of 40. This comprehensive guide explores various methods, real-world applications, and provides numerous examples to solidify your understanding.
Calculating the Percentage: The Basic Method
The most straightforward method to determine what percent 12 is of 40 involves a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 12
- Whole: 40
Substituting these values into the formula:
(12 / 40) * 100% = 30%
Therefore, 12 is 30% of 40.
This basic formula is the foundation for understanding and calculating percentages across diverse scenarios. Let's explore some variations and alternative approaches.
Alternative Calculation Methods: Providing Flexibility and Understanding
While the above method is efficient, understanding alternative methods can enhance comprehension and problem-solving skills. Let's examine a few:
-
Using Proportions: This method relies on setting up a proportion to solve for the unknown percentage. We can represent the problem as:
12/40 = x/100
To solve for 'x', we cross-multiply:
40x = 1200
x = 1200 / 40
x = 30
Therefore, x = 30%, confirming our previous result. This method is particularly useful when dealing with more complex percentage problems.
-
Using Decimal Equivalents: We can convert the fraction 12/40 into a decimal by dividing 12 by 40:
12 / 40 = 0.3
To convert this decimal to a percentage, simply multiply by 100%:
0.3 * 100% = 30%
This method highlights the close relationship between decimals and percentages.
Real-World Applications: Percentages in Everyday Life
Percentages are ubiquitous in our daily lives. Understanding their calculation is essential for navigating various situations effectively. Here are some practical examples:
-
Sales and Discounts: A common application is calculating discounts offered during sales. If a store offers a 20% discount on a $50 item, the discount amount is calculated as (20/100) * $50 = $10. The final price would be $50 - $10 = $40.
-
Taxes and Tips: Calculating sales tax or service tips involves percentages. If the sales tax is 6% on a $100 purchase, the tax amount is (6/100) * $100 = $6. The total cost would be $100 + $6 = $106. Similarly, a 15% tip on a $75 meal would be (15/100) * $75 = $11.25.
-
Financial Statements and Budgeting: Percentages are fundamental in analyzing financial statements, such as profit margins, expense ratios, and debt-to-equity ratios. Understanding these percentages allows individuals and businesses to make informed financial decisions. For instance, a profit margin of 10% indicates that 10% of revenue is profit.
-
Statistical Analysis and Data Interpretation: Percentages are crucial for representing and interpreting statistical data. Survey results, election polls, and economic indicators are often presented as percentages to simplify the understanding of large datasets. For example, if 60% of respondents in a survey favored a particular policy, it signifies a strong majority.
-
Grade Calculations: In education, percentages are used to calculate grades. If a student scores 80 out of 100 on an exam, their grade is 80%. This percentage representation simplifies the comparison of performance across different exams or assignments.
-
Interest Rates and Loans: Interest rates on loans and investments are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions regarding borrowing or investing. For example, an interest rate of 5% on a $1000 loan means an annual interest payment of $50.
-
Commission and Bonuses: Sales commissions and performance bonuses are often calculated as a percentage of sales or revenue. A salesperson earning a 5% commission on $20,000 in sales would receive (5/100) * $20,000 = $1000.
Solving More Complex Percentage Problems
The principles discussed above can be extended to tackle more complex percentage problems. Let's consider a few examples:
Example 1: What is 15% of 250?
Using the formula (Part/Whole) * 100% = Percentage, we can rearrange it to solve for the "Part":
Part = (Percentage/100%) * Whole
Part = (15/100) * 250 = 37.5
Therefore, 15% of 250 is 37.5.
Example 2: If 20% of a number is 50, what is the number?
Let the number be 'x'. We can set up the equation:
(20/100) * x = 50
0.2x = 50
x = 50 / 0.2
x = 250
Therefore, the number is 250.
Example 3: A shirt is on sale for $30 after a 25% discount. What was the original price?
Let the original price be 'x'. The sale price is 75% (100% - 25%) of the original price. Therefore:
0.75x = 30
x = 30 / 0.75
x = 40
The original price of the shirt was $40.
Percentage Increase and Decrease
Understanding percentage increase and decrease is also important. These are calculated as follows:
-
Percentage Increase: [(New Value - Old Value) / Old Value] * 100%
-
Percentage Decrease: [(Old Value - New Value) / Old Value] * 100%
For example, if a stock price increases from $50 to $60, the percentage increase is [(60-50)/50] * 100% = 20%. If the price decreases from $60 to $48, the percentage decrease is [(60-48)/60] * 100% = 20%.
Conclusion: Mastering Percentages for Success
This comprehensive guide has explored the fundamental concepts of percentage calculations and illustrated their practical applications in various aspects of daily life. By understanding the basic formula, alternative methods, and diverse examples provided, readers can confidently tackle percentage problems of varying complexity. The ability to calculate and interpret percentages is a valuable skill that empowers individuals to make informed decisions in personal finance, professional endeavors, and everyday situations. From understanding discounts at the mall to interpreting complex financial reports, mastering percentages is crucial for navigating the modern world successfully. Remember to practice regularly, and you'll soon become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
How Many Inches In 12 Meters
Apr 24, 2025
-
How Does Hydrosphere Interact With Biosphere
Apr 24, 2025
-
What Is 167 Cm In Inches
Apr 24, 2025
-
21 8 As A Mixed Number
Apr 24, 2025
-
Who Developed The Law Of Conservation Of Mass
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 12 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.