What Percent Is 13 Of 20
Kalali
Apr 15, 2025 · 5 min read
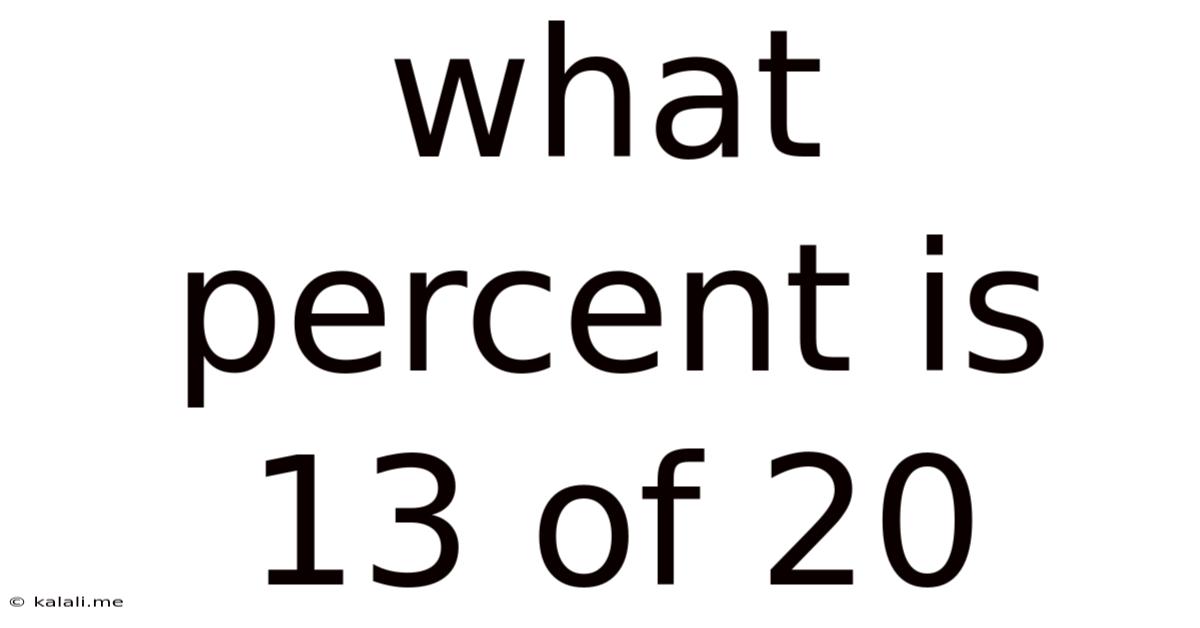
Table of Contents
What Percent is 13 of 20? A Deep Dive into Percentage Calculations and Their Applications
Finding what percent 13 is of 20 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept crucial in various fields, from finance and statistics to everyday life. This article will not only answer the question directly but also explore the underlying principles, provide multiple calculation methods, and illustrate practical applications of percentage calculations. We'll delve into the theory, offer alternative approaches, and showcase the relevance of percentages in real-world scenarios.
Meta Description: Learn how to calculate what percent 13 is of 20. This comprehensive guide explores various methods, explains the underlying principles, and showcases real-world applications of percentage calculations. Master percentages and improve your mathematical skills!
Understanding Percentages: The Foundation
A percentage is a fraction expressed as a number out of 100. It represents a proportion of a whole. The symbol "%" denotes percentage. The phrase "x percent of y" translates mathematically to (x/100) * y. Understanding this fundamental relationship is key to solving percentage problems efficiently.
Calculating What Percent 13 is of 20: The Direct Approach
The most straightforward method involves setting up a proportion:
13/20 = x/100
Here:
- 13 represents the part.
- 20 represents the whole.
- x represents the unknown percentage.
To solve for x, we cross-multiply:
20x = 1300
Then, divide both sides by 20:
x = 65
Therefore, 13 is 65% of 20.
Alternative Methods: Exploring Different Approaches
While the direct proportion method is efficient, exploring alternative methods deepens our understanding and provides flexibility in tackling different percentage problems.
Method 1: Using Decimal Conversion
First, express the fraction 13/20 as a decimal:
13 ÷ 20 = 0.65
Then, multiply the decimal by 100 to convert it to a percentage:
0.65 * 100 = 65%
This method is particularly useful when dealing with calculators, as it simplifies the calculation process.
Method 2: Using the Formula (Part/Whole) * 100%
This is a concise formula encapsulating the core principle of percentage calculations. Substituting our values:
(13/20) * 100% = 65%
This method highlights the direct relationship between the part, the whole, and the resulting percentage.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous, impacting numerous aspects of daily life and professional endeavors. Here are some examples:
1. Finance:
- Interest rates: Banks and financial institutions use percentages to calculate interest on loans, savings accounts, and investments. Understanding percentage calculations is crucial for making informed financial decisions, comparing loan offers, and tracking investment growth.
- Discounts and sales: Retailers frequently advertise discounts as percentages (e.g., "20% off"). Calculating the actual price reduction requires understanding percentage calculations.
- Taxes: Sales tax, income tax, and property tax are expressed as percentages. Accurately calculating these taxes relies on a clear understanding of percentage computations.
- Investment returns: Investment returns are often expressed as percentages, reflecting the growth or decline of an investment over a specific period. Understanding percentage change helps investors analyze their portfolio performance.
2. Statistics:
- Data analysis: Percentages are essential tools in data analysis. They help to present data concisely, showing proportions and trends within datasets. For example, expressing survey results as percentages makes it easier to understand and compare different responses.
- Probability: Percentage is often used to represent probabilities. For instance, a 75% chance of rain implies that there's a 75 out of 100 probability of rain.
- Statistical significance: In statistical hypothesis testing, percentages are used to determine the significance of results.
3. Everyday Life:
- Tipping: Calculating tips in restaurants often involves determining a certain percentage of the bill amount.
- Cooking: Recipes frequently list ingredients as percentages of the total weight or volume.
- Sales commissions: Sales professionals often earn a commission based on a percentage of their sales.
4. Science and Engineering:
- Efficiency: In engineering, efficiency is often expressed as a percentage. For example, the efficiency of an engine might be given as 80%, meaning that 80% of the input energy is converted into useful work.
- Error analysis: Scientists and engineers use percentages to represent errors or uncertainties in measurements and calculations.
Expanding Our Understanding: Percentage Increase and Decrease
While our initial problem focuses on finding a percentage of a whole, it's essential to understand related concepts like percentage increase and decrease.
Percentage Increase: This represents the relative change when a value increases. The formula is:
[(New Value - Original Value) / Original Value] * 100%
Percentage Decrease: This represents the relative change when a value decreases. The formula is:
[(Original Value - New Value) / Original Value] * 100%
Understanding these concepts is vital for analyzing changes in data over time, such as population growth, stock prices, or economic indicators.
Addressing Potential Errors and Misconceptions
Common mistakes in percentage calculations include:
- Incorrectly interpreting the "whole": Ensuring you're using the correct base value (the "whole") is crucial for accurate results.
- Mixing up percentages and decimals: Remember to convert between percentages and decimals correctly using multiplication or division by 100.
- Rounding errors: While rounding can simplify calculations, be aware of the potential accumulation of errors in complex calculations.
Conclusion: Mastering Percentages for a More Numerate World
This in-depth exploration of percentage calculations reveals their significance in various contexts. Learning to accurately calculate and interpret percentages is a fundamental skill that enhances decision-making abilities across various domains. By understanding the underlying principles and applying different calculation methods, you can confidently approach percentage problems and harness their power in solving real-world challenges. Remember that practice is key to mastering percentage calculations – the more you practice, the more confident and proficient you will become. From navigating financial transactions to interpreting data effectively, a solid understanding of percentages empowers you to make informed choices and become more numerate in an increasingly data-driven world.
Latest Posts
Latest Posts
-
How Much Can I Sell Bro For
Jul 02, 2025
-
How Many Bottles Is 64 Oz Of Water
Jul 02, 2025
-
How Many Ounces In Pound Of Meat
Jul 02, 2025
-
What Is The Diameter Of A Quarter
Jul 02, 2025
-
Spoon Gets Hot In A Bowl Of Soup
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 13 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.