What Percent Is 2 Of 12
Kalali
Apr 08, 2025 · 5 min read
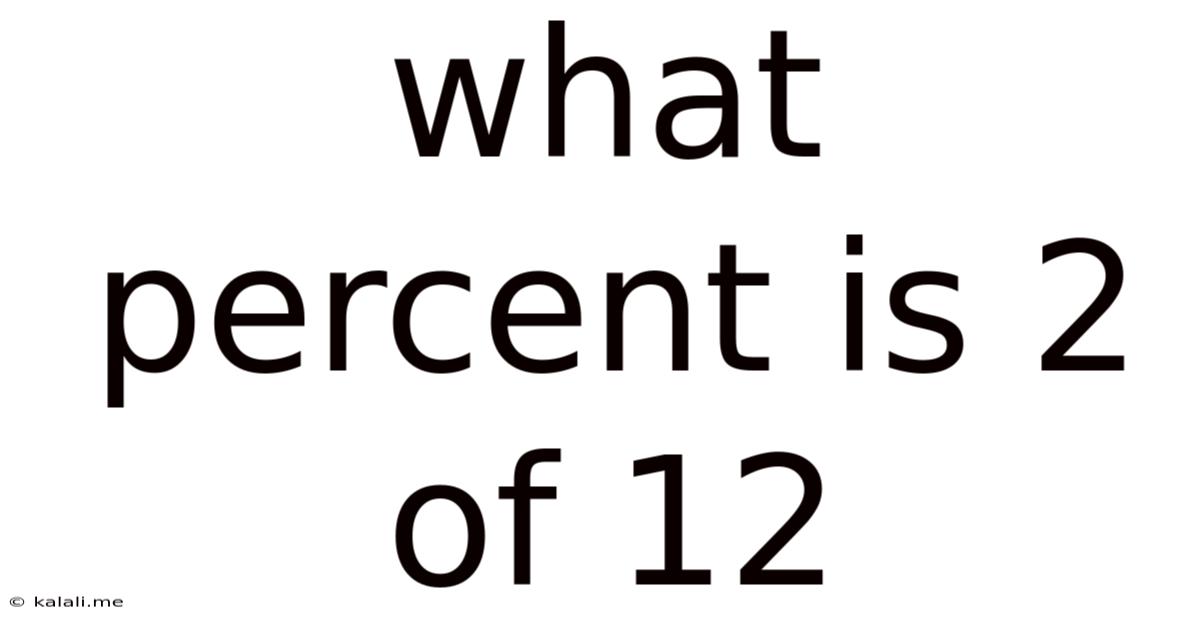
Table of Contents
What Percent is 2 of 12? A Deep Dive into Percentages and Their Applications
Meta Description: Uncover the answer to "What percent is 2 of 12?" and delve into the world of percentages. Learn the calculation method, explore real-world applications, and master percentage problems with practical examples and explanations.
Finding the percentage one number represents of another is a fundamental mathematical concept with widespread applications in everyday life, from calculating discounts and tax rates to understanding statistics and financial data. This article will thoroughly explore how to determine what percent 2 is of 12, providing a step-by-step guide and expanding on the broader concept of percentages and their practical use.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol used to represent percentages is "%". Essentially, a percentage shows the proportion of one quantity relative to another, expressing it as a part per hundred. This makes percentages a standardized and easily comparable way to represent proportions. For example, 50% represents 50 out of 100, which simplifies to 1/2 or one-half.
Calculating "What Percent is 2 of 12?"
The calculation is straightforward and can be approached using two primary methods:
Method 1: Using a Fraction and Conversion
-
Express the relationship as a fraction: The problem "What percent is 2 of 12?" can be written as the fraction 2/12.
-
Simplify the fraction (optional but recommended): Both the numerator (2) and the denominator (12) are divisible by 2. Simplifying the fraction gives us 1/6.
-
Convert the fraction to a decimal: Divide the numerator (1) by the denominator (6). This gives us 0.166666... (a repeating decimal).
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%). 0.166666... x 100 ≈ 16.67%.
Therefore, 2 is approximately 16.67% of 12.
Method 2: Using a Proportion
This method uses the concept of proportions to solve for the unknown percentage. We set up a proportion where we know one ratio (2/12) and the other ratio is expressed as the percentage (x/100). This results in:
2/12 = x/100
To solve for x (the percentage), we cross-multiply:
12x = 200
Now, divide both sides by 12:
x = 200/12 = 16.6666...
Again, converting to a percentage by multiplying by 100 gives us approximately 16.67%.
Practical Applications of Percentages
The ability to calculate percentages is crucial in numerous everyday scenarios:
1. Financial Calculations:
- Discounts: Retail stores frequently advertise discounts as percentages. For example, a 20% discount on a $100 item means a reduction of $20 (20% of $100).
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the purchase price or income.
- Interest Rates: Interest on loans, savings accounts, and investments is calculated as a percentage of the principal amount.
- Investment Returns: The performance of investments is often measured using percentage returns. A 10% return on a $1000 investment means a profit of $100.
- Profit Margins: Businesses use percentage to calculate their profit margin - the percentage of revenue that represents profit after deducting costs.
2. Statistical Analysis:
- Data Representation: Percentages are extensively used to present data in a clear and concise manner, particularly in charts and graphs. For example, survey results are often expressed as percentages of the total respondents.
- Probability: The likelihood of an event occurring is often expressed as a percentage probability.
- Growth and Decline: Percentage change is frequently used to describe the growth or decline of a quantity over time (e.g., population growth, economic growth, sales growth).
3. Everyday Life:
- Tipping: Calculating tips in restaurants is often done as a percentage of the bill (e.g., 15% or 20% tip).
- Cooking and Baking: Recipes frequently use percentages to indicate the ratio of ingredients.
- Grading Systems: Many educational systems use percentages to represent grades and scores.
Further Exploring Percentages: Advanced Concepts
Beyond the basic calculations, several other important percentage-related concepts warrant exploration:
-
Percentage Increase/Decrease: This calculates the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] x 100. A positive result indicates an increase, while a negative result indicates a decrease.
-
Percentage Points: Percentage points represent the difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Compound Interest: This involves earning interest not only on the principal amount but also on the accumulated interest from previous periods. It's a more complex calculation and is used extensively in financial applications.
-
Working with Percentages in Spreadsheets and Software: Most spreadsheet software packages (like Microsoft Excel or Google Sheets) have built-in functions to simplify percentage calculations, such as calculating percentage changes, finding percentages of values, and more.
Practice Problems
To solidify your understanding, try solving these problems:
- What percent is 5 of 20?
- What is 30% of 80?
- A shirt is originally priced at $50 and is discounted by 15%. What is the sale price?
- A student scored 85 out of 100 on a test. What is their percentage score?
- The population of a city increased from 10,000 to 12,000. What is the percentage increase?
By working through these examples, you'll reinforce your understanding of percentage calculations and their diverse applications.
Conclusion
Understanding percentages is a valuable skill with far-reaching applications. This article has provided a comprehensive guide to calculating percentages, explained the significance of this mathematical concept, and explored its practical use in various contexts. Mastering percentages will enhance your ability to interpret data, make informed financial decisions, and navigate various aspects of daily life with greater confidence. Remember to practice regularly to build your proficiency and apply these concepts to real-world problems.
Latest Posts
Latest Posts
-
Half A Pint Is How Many Cups
Apr 17, 2025
-
What Is A 22 Out Of 26
Apr 17, 2025
-
Cuanto Es 17 Centimetros En Pulgadas
Apr 17, 2025
-
How Many Pints In 2 Gallons
Apr 17, 2025
-
How Many Hours Is 111 Minutes
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 2 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.