What Percent Is 2 Of 15
Kalali
Apr 04, 2025 · 5 min read
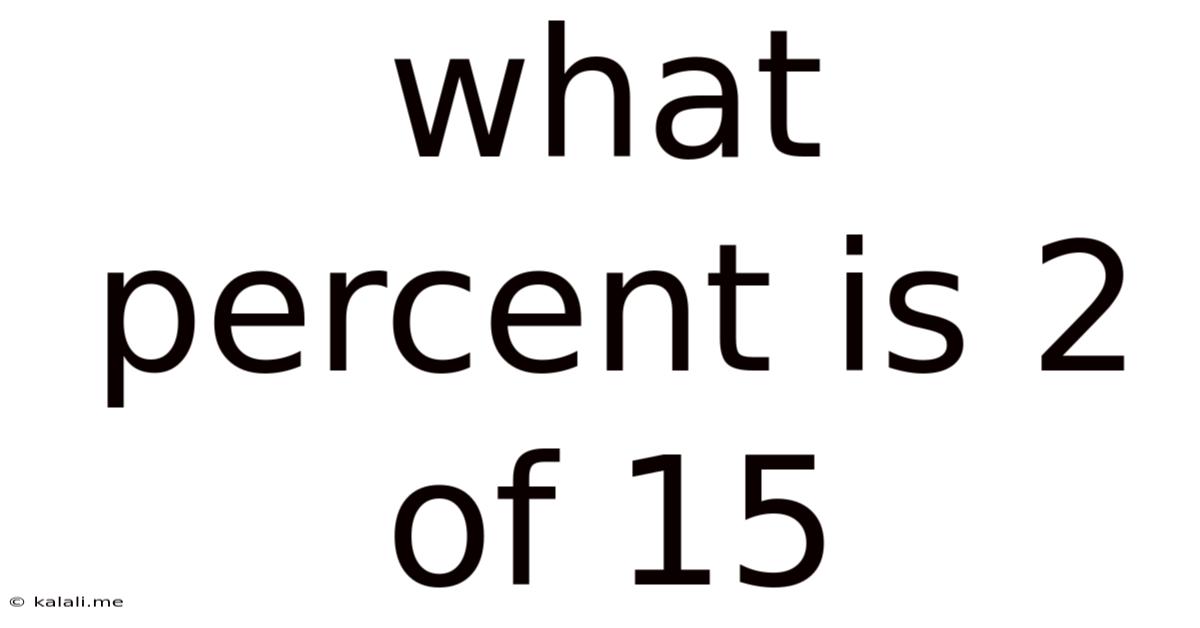
Table of Contents
What Percent is 2 of 15? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine what percent one number represents of another is crucial for making informed decisions and interpreting data effectively. This article delves into the calculation of "What percent is 2 of 15?", providing a step-by-step explanation, exploring various methods, and offering practical examples to solidify your understanding.
Understanding Percentages
Before diving into the specific calculation, let's establish a solid understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Percentages are used to express proportions or ratios in a standardized and easily comparable format. They provide a concise way to represent parts of a whole. Understanding percentages is essential for interpreting data presented in charts, graphs, and reports across numerous fields.
Method 1: Using the Percentage Formula
The most straightforward way to determine what percent 2 is of 15 is to use the fundamental percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 2 (the number we want to express as a percentage)
- Whole: 15 (the total number)
Substituting these values into the formula, we get:
(2 / 15) x 100 = Percentage
Calculating the fraction first:
2 / 15 ≈ 0.1333
Now, multiply the result by 100:
0.1333 x 100 ≈ 13.33%
Therefore, 2 is approximately 13.33% of 15.
Method 2: Using Proportions
Another approach involves setting up a proportion. A proportion is an equation that states that two ratios are equal. We can set up a proportion to solve for the percentage:
x / 100 = 2 / 15
Where 'x' represents the percentage we are trying to find. To solve for x, we can cross-multiply:
15x = 200
Now, divide both sides by 15:
x = 200 / 15
x ≈ 13.33
Therefore, 2 is approximately 13.33% of 15.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the calculation. Simply divide 2 by 15 and then multiply the result by 100. The calculator will directly provide the percentage value, typically showing 13.33%.
Practical Applications of Percentage Calculations
The ability to calculate percentages has numerous practical applications in everyday life and professional settings. Here are a few examples:
1. Shopping and Sales:
Understanding percentages is essential when shopping, especially during sales. If a store offers a 20% discount on an item, you can easily calculate the final price by finding 20% of the original price and subtracting it.
2. Budgeting and Finance:
Percentages play a vital role in budgeting and financial planning. Tracking your spending as percentages of your income allows you to see where your money is going and identify areas for potential savings. Calculating interest rates and loan repayments also heavily relies on percentage calculations.
3. Grades and Assessments:
In education, grades and assessment scores are often represented as percentages. Understanding your percentage score on a test allows you to gauge your performance against the total possible points.
4. Data Analysis and Statistics:
Percentages are frequently used in data analysis to represent proportions within a dataset. For instance, market research reports often express market share as percentages, providing a quick way to compare different companies or products.
5. Scientific Research:
Percentage calculations are vital in various scientific fields. For example, determining the percentage of a specific element in a compound or the percentage change in a population over time all involve percentage calculations.
Expanding on Percentage Concepts: Beyond the Basics
While calculating "What percent is 2 of 15?" provides a fundamental understanding, let's explore some related percentage concepts:
1. Finding the Percentage Increase or Decrease:
Calculating percentage change is important when comparing values over time. The formula is:
((New Value - Old Value) / Old Value) x 100 = Percentage Change
A positive result indicates a percentage increase, while a negative result indicates a percentage decrease.
2. Calculating a Percentage of a Number:
This involves finding a specific percentage of a given number. For example, to find 25% of 80, you would multiply 80 by 0.25 (which is the decimal equivalent of 25%).
3. Finding the Original Value After a Percentage Change:
If you know the final value and the percentage change, you can work backward to find the original value. This requires some algebraic manipulation of the percentage change formula.
4. Working with Compound Percentages:
Compound percentages involve applying a percentage change multiple times. For instance, calculating compound interest involves applying the interest rate repeatedly over a period of time.
Common Mistakes to Avoid When Calculating Percentages
Several common mistakes can lead to incorrect percentage calculations. Be mindful of the following:
- Incorrect Order of Operations: Always perform division before multiplication when using the percentage formula.
- Rounding Errors: Rounding off intermediate results too early can introduce inaccuracies in the final answer.
- Misinterpreting the Problem: Carefully read the problem to correctly identify the "part" and the "whole" before applying the formula.
Conclusion
Calculating "What percent is 2 of 15?" is a simple yet fundamental skill with widespread applications. Understanding various methods, including the percentage formula, proportions, and using a calculator, empowers you to tackle diverse percentage-related problems. Mastering these concepts enhances your ability to interpret data, make informed decisions, and succeed in various aspects of life, from personal finance to professional endeavors. Remember to practice regularly and carefully review the concepts to build confidence and accuracy in your calculations. The more you practice, the more intuitive percentage calculations will become.
Latest Posts
Latest Posts
-
How Hot Is 38 Degrees Celsius
Apr 11, 2025
-
An Ice Cube Contains A Large Air Bubble
Apr 11, 2025
-
How Many Centimeters Is 8 Ft
Apr 11, 2025
-
60 Degrees Fahrenheit Equals What In Celsius
Apr 11, 2025
-
Least Common Multiple Of 20 And 15
Apr 11, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 2 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.