What Percent Is 2 Of 8
Kalali
Apr 07, 2025 · 5 min read
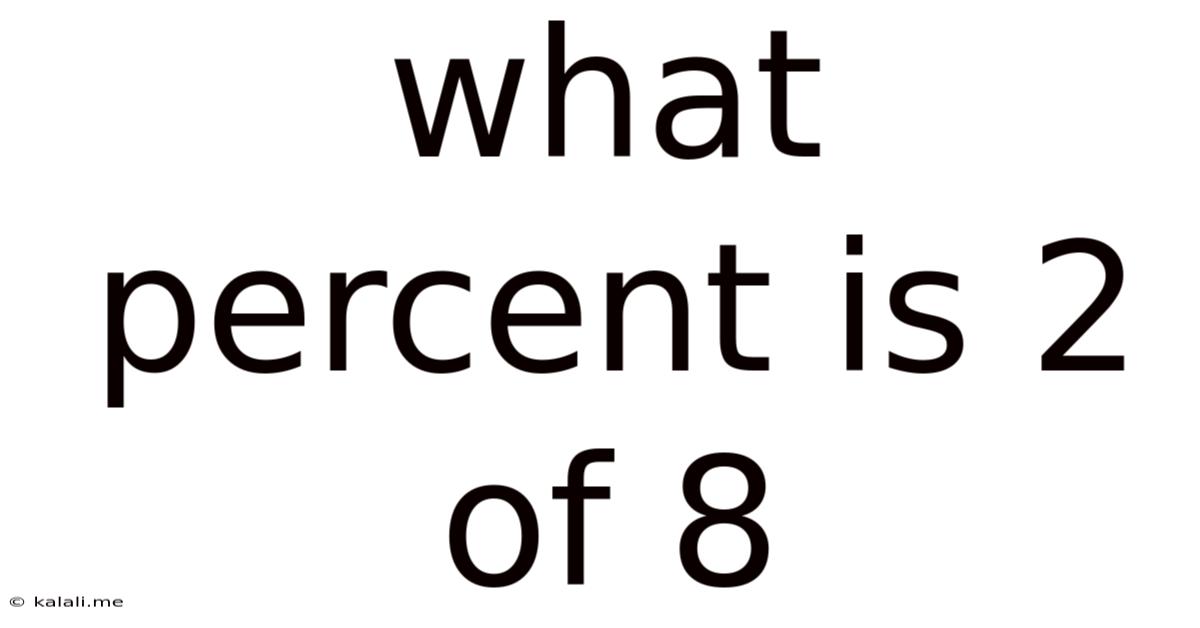
Table of Contents
What Percent is 2 of 8? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and tips to comprehending financial reports and statistical data. This article delves into the seemingly simple question, "What percent is 2 of 8?", providing a detailed explanation of the process, exploring different calculation methods, and expanding on the broader context of percentage calculations.
Understanding Percentages: The Basics
Before tackling the specific problem, let's establish a clear understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
The core concept lies in representing a portion of a whole as a fraction of 100. This allows for easy comparison and understanding of proportions across different datasets.
Method 1: Using the Formula
The most straightforward method to determine what percent 2 is of 8 involves a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 2 (the smaller number)
- Whole: 8 (the larger number)
Substituting these values into the formula:
(2 / 8) * 100% = 25%
Therefore, 2 is 25% of 8.
Method 2: Simplifying the Fraction
Alternatively, we can simplify the fraction before multiplying by 100%. The fraction 2/8 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
2 / 8 = 1 / 4
Now, we can convert the simplified fraction to a percentage:
(1 / 4) * 100% = 25%
This method showcases the equivalence between different fractional representations, reinforcing the concept of proportional relationships.
Method 3: Using Proportions
The problem can also be solved using proportions. We can set up a proportion to find the equivalent percentage:
2/8 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
8x = 200
x = 200 / 8
x = 25
Therefore, x = 25%, confirming our previous results. This method highlights the proportional relationship between the part and the whole, expressed as a percentage.
Expanding the Concept: Real-world Applications
The ability to calculate percentages has far-reaching applications in various aspects of daily life:
1. Finance and Budgeting:
- Calculating discounts: If a store offers a 20% discount on an item priced at $50, calculating the discount amount (20% of $50) and the final price is crucial.
- Understanding interest rates: Interest calculations, whether for loans or savings accounts, rely heavily on percentage calculations.
- Analyzing financial statements: Interpreting financial reports involving profit margins, revenue growth, and expense ratios requires proficiency in percentage analysis.
2. Statistics and Data Analysis:
- Representing proportions: Percentages are invaluable for representing portions of a whole in data analysis, such as demographics or survey results.
- Calculating percentages changes: Tracking changes over time (e.g., population growth, sales increase) often involves calculating percentage changes.
- Understanding probabilities: Expressing probabilities as percentages (e.g., a 75% chance of rain) is common in everyday life and in statistical modeling.
3. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in a restaurant involves calculating a percentage of the total bill.
- Understanding tax rates: Calculating sales tax or income tax involves applying a percentage to the taxable amount.
- Comparing prices: Comparing prices of different items with varying sizes or quantities often requires calculating percentages to determine the best value.
Advanced Percentage Calculations: Beyond the Basics
While the example of "What percent is 2 of 8?" provides a foundational understanding, let's explore some more advanced percentage calculations:
1. Percentage Increase and Decrease:
Calculating the percentage increase or decrease between two values involves finding the difference between the two values, dividing it by the original value, and then multiplying by 100%.
For example, if a value increases from 10 to 15, the percentage increase is:
((15 - 10) / 10) * 100% = 50%
2. Finding the Original Value:
If you know the percentage and the final value, you can work backward to find the original value. For example, if a value after a 20% increase is $60, the original value can be calculated as:
$60 / 1.20 = $50
3. Percentage Points vs. Percentages:
It's crucial to distinguish between percentage points and percentages. A change of 10 percentage points means a direct difference of 10%, while a 10% increase from, say, 20% would result in 22%, a difference of only 2 percentage points. This distinction is important for accurate interpretation of data.
Mastering Percentage Calculations: Tips and Tricks
To improve proficiency in percentage calculations:
- Practice regularly: Consistent practice is key to mastering any mathematical skill.
- Use different methods: Experiment with various methods (formula, proportions, simplification) to find the approach that best suits your understanding.
- Check your work: Always double-check your calculations to ensure accuracy.
- Utilize online resources: Numerous online calculators and tutorials are available to assist with percentage calculations.
- Relate to real-world examples: Apply your knowledge to real-life scenarios to reinforce understanding and improve retention.
Conclusion: The Power of Percentages
The seemingly simple question, "What percent is 2 of 8?", opens the door to a vast understanding of percentage calculations and their widespread applications. From basic arithmetic to advanced financial analysis, mastering percentages is a skill that empowers individuals to interpret data, make informed decisions, and navigate various aspects of life with confidence. By understanding the underlying principles and employing different calculation methods, anyone can confidently tackle percentage problems and harness the power of this fundamental mathematical tool.
Latest Posts
Latest Posts
-
What Does The Diaphragm Do In A Microscope
Apr 10, 2025
-
What Is 175 Degrees Celsius In Fahrenheit
Apr 10, 2025
-
25 Meters Is How Many Centimeters
Apr 10, 2025
-
How Many Cups In 150 Ml
Apr 10, 2025
-
Lines Of Symmetry In A Circle
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 2 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.