What Percent Is 2 Out Of 6
Kalali
Apr 10, 2025 · 5 min read
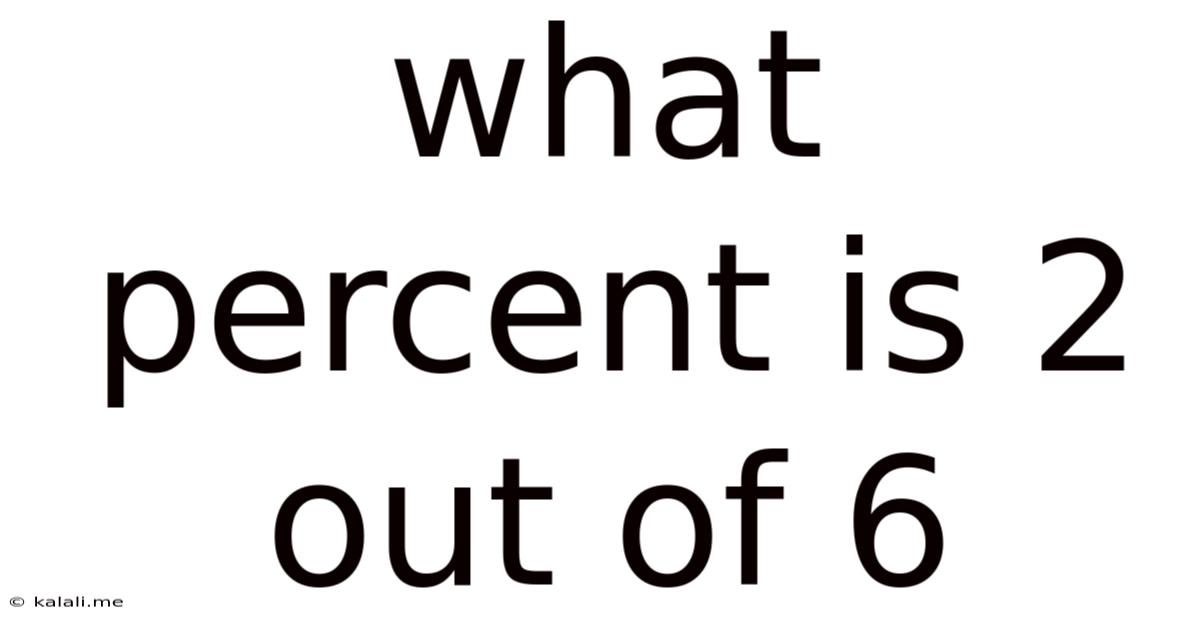
Table of Contents
What Percent is 2 out of 6? A Deep Dive into Percentage Calculations and Real-World Applications
What percent is 2 out of 6? This seemingly simple question opens the door to a broader understanding of percentages, their calculations, and their widespread applications in everyday life. This article will not only answer the initial question but will also explore the underlying mathematical principles, different calculation methods, and practical examples demonstrating the usefulness of percentage calculations across various fields.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (from the Latin per centum). It's a crucial tool for comparing proportions, representing changes, and expressing ratios in a standardized and easily understandable format. Understanding percentages is fundamental to many aspects of life, from finance and shopping to statistics and scientific analysis.
Calculating "What Percent is 2 out of 6?"
The core of solving "what percent is 2 out of 6?" lies in converting the fraction 2/6 into a percentage. We can achieve this through several methods:
Method 1: Direct Conversion
This method involves converting the fraction to a decimal and then multiplying by 100.
- Convert the fraction to a decimal: 2 divided by 6 equals 0.3333... (repeating decimal).
- Multiply by 100: 0.3333... * 100 = 33.33...%
Therefore, 2 out of 6 is approximately 33.33%. The repeating decimal indicates that this percentage is a recurring value. For most practical purposes, rounding to two decimal places (33.33%) is sufficient.
Method 2: Simplifying the Fraction First
This method involves simplifying the fraction before converting it to a percentage. Simplifying often makes the calculation easier.
- Simplify the fraction: 2/6 can be simplified to 1/3 by dividing both the numerator and denominator by their greatest common divisor (2).
- Convert the simplified fraction to a decimal: 1 divided by 3 equals 0.3333...
- Multiply by 100: 0.3333... * 100 = 33.33...%
This method yields the same result, demonstrating that simplifying the fraction doesn't alter the percentage.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We set up a proportion where x represents the percentage we're looking for:
2/6 = x/100
To solve for x, we cross-multiply:
6x = 200
x = 200/6
x ≈ 33.33%
Beyond the Basic Calculation: Understanding the Context
While the calculation itself is straightforward, understanding the context in which this percentage arises is crucial. For example:
- Test Scores: If a student answered 2 out of 6 questions correctly on a quiz, their score is 33.33%.
- Survey Results: If 2 out of 6 respondents chose a particular option in a survey, that option received 33.33% of the votes.
- Inventory Management: If 2 out of 6 items in a stock are defective, 33.33% of the items are defective.
- Probability: If there's a 2 out of 6 chance of an event occurring, the probability of that event is 33.33%.
The interpretation of the 33.33% result depends heavily on the specific situation.
Real-World Applications of Percentage Calculations
Percentages are ubiquitous in various aspects of daily life and professional fields. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage increases and decreases is crucial for managing personal finances and making informed investment decisions. For example, understanding compound interest requires a strong grasp of percentage calculations.
-
Retail and Sales: Discounts are commonly expressed as percentages (e.g., a 20% discount). Sales tax is also calculated as a percentage of the purchase price. Analyzing sales data and understanding sales trends often involve percentage changes. Calculating markups and profit margins are also essential for businesses.
-
Statistics and Data Analysis: Percentages are used extensively in statistical analysis to represent proportions, probabilities, and changes in data. Understanding percentage distributions, frequency distributions, and relative frequencies is crucial for interpreting data effectively. Statistical significance testing often utilizes percentage-based metrics.
-
Healthcare: Many healthcare metrics are expressed as percentages. For instance, the survival rate of a disease, the success rate of a treatment, or the prevalence of a condition within a population are often presented as percentages. Understanding these percentages is vital for making informed healthcare decisions.
-
Science: Percentage calculations are used in numerous scientific fields. For example, determining the percentage composition of a chemical compound, calculating the percentage yield of a chemical reaction, or representing the percentage of a specific element in a sample all require percentage calculations.
-
Education: Grading systems, performance assessments, and statistical analysis of educational data heavily rely on percentage calculations. Understanding student performance and tracking progress often involves interpreting percentages.
Advanced Percentage Calculations
Beyond the basic calculation of "what percent is 2 out of 6?", there are more complex percentage problems:
-
Finding the Percentage Increase or Decrease: Calculating the percentage change between two values requires understanding the formula: [(New Value - Old Value) / Old Value] * 100. This is crucial for tracking trends, analyzing growth, and understanding changes over time.
-
Finding a Percentage of a Number: Determining a specific percentage of a given number is frequently used in discounts, tax calculations, and commission calculations. For example, finding 15% of $50 involves multiplying 50 by 0.15.
-
Finding the Original Amount after a Percentage Change: If you know the final amount after a percentage increase or decrease, you can work backward to find the original amount. This involves using algebraic equations to solve for the unknown value.
-
Working with Compound Percentages: Compound percentages involve applying a percentage change repeatedly. This is commonly seen in compound interest calculations.
Conclusion: Mastering Percentages for Success
The seemingly simple question, "What percent is 2 out of 6?" opens the door to a world of practical applications and mathematical concepts surrounding percentages. Mastering percentage calculations is a valuable skill that enhances problem-solving abilities across various disciplines. From personal finance to scientific research, understanding percentages provides a crucial framework for interpreting data, making informed decisions, and navigating the numerical complexities of the modern world. By understanding the different calculation methods and their applications, individuals can confidently tackle a wide range of percentage-related problems and apply this knowledge to improve their understanding of data and make more informed choices in various aspects of life.
Latest Posts
Latest Posts
-
How Many Ounces Is 1 3 Cup Liquid
Apr 18, 2025
-
How Many Degrees Is 200 Celsius
Apr 18, 2025
-
How Many Vertices Does A Trapezium Have
Apr 18, 2025
-
What Is The Highest Common Factor Of 20 And 30
Apr 18, 2025
-
What Is 230 Cm In Feet
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 2 Out Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.