What Percent Is 22 Of 40
Kalali
Apr 26, 2025 · 5 min read
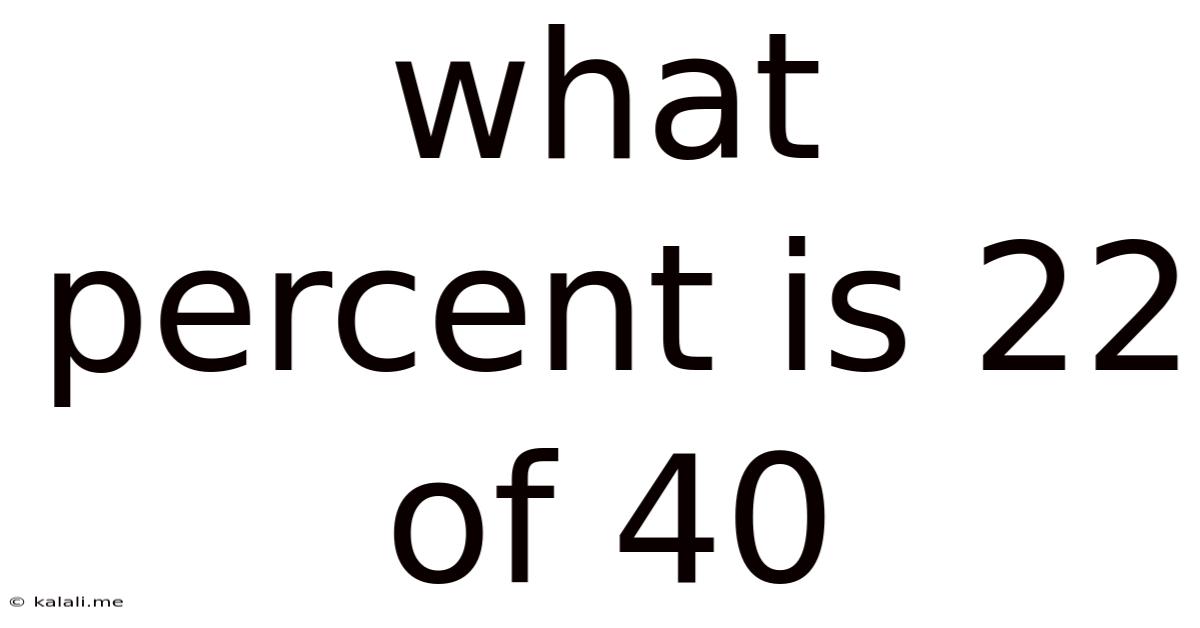
Table of Contents
What Percent is 22 of 40? A Deep Dive into Percentage Calculations and Applications
What percent is 22 of 40? This seemingly simple question opens the door to a world of percentage calculations, their applications in everyday life, and even some advanced mathematical concepts. Understanding percentages is crucial for everything from calculating discounts and sales tax to comprehending financial reports and analyzing statistical data. This article will not only answer the initial question but will also explore the underlying principles, provide various methods for solving similar problems, and discuss real-world applications of percentage calculations.
Meta Description: Learn how to calculate percentages, understand the concept of "what percent is 22 of 40?", explore different calculation methods, and discover real-world applications of percentage calculations in finance, statistics, and everyday life.
First, let's tackle the core question: What percent is 22 of 40?
The most straightforward approach involves using the following formula:
(Part / Whole) * 100% = Percentage
In this case:
(22 / 40) * 100% = 55%
Therefore, 22 is 55% of 40.
Understanding the Fundamentals of Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. Percentages are a convenient way to represent proportions or parts of a whole. They provide a standardized way to compare different quantities, making it easier to understand and analyze data.
Consider the example above: 22 out of 40. We can express this as a fraction (22/40), a decimal (0.55), or a percentage (55%). All three represent the same proportion.
Different Methods for Calculating Percentages
While the basic formula is straightforward, several methods can be used to calculate percentages, depending on the context and the tools available:
1. Using the Basic Formula:
This method, already demonstrated above, is the most fundamental and widely applicable. It's perfect for simple percentage calculations. Simply divide the part by the whole and multiply by 100%.
2. Using Proportions:
Proportions offer a slightly different approach to solving percentage problems. You can set up a proportion:
x/100 = 22/40
To solve for x (the percentage), cross-multiply and solve the equation:
40x = 2200
x = 2200/40 = 55
Therefore, x = 55%, confirming our previous result. This method is particularly useful when dealing with more complex percentage problems.
3. Using Decimal Conversion:
Converting the fraction to a decimal provides another route to calculating percentages. Divide the part by the whole:
22 / 40 = 0.55
Then, multiply the decimal by 100% to convert it to a percentage:
0.55 * 100% = 55%
This method is efficient and can be easily performed using a calculator.
4. Using a Calculator:
Modern calculators have built-in percentage functions that simplify the process considerably. Many calculators have a "%" button that directly calculates percentages. Simply enter the numbers and use the percentage function to get the result.
Real-World Applications of Percentage Calculations
Percentages are used extensively across various fields:
1. Finance:
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding interest rates is crucial for making informed financial decisions.
- Investment Returns: Investors use percentages to track the performance of their investments. Percentage changes in stock prices, bond yields, and other investments are frequently reported.
- Sales Tax: Sales tax is calculated as a percentage of the purchase price.
- Discounts and Markups: Retailers use percentages to offer discounts and mark up prices. Calculating discounts and the final price after a discount involves percentage calculations.
- Compound Interest: Understanding compound interest, which involves calculating interest on both the principal and accumulated interest, requires a thorough understanding of percentages.
2. Statistics:
- Data Analysis: Percentages are frequently used to represent proportions and distributions within datasets. Statistical analysis often involves calculating percentages to summarize and interpret data.
- Probability: Probability is often expressed as a percentage, indicating the likelihood of an event occurring.
- Surveys and Polls: Survey results are typically presented as percentages to make it easier to understand the distribution of opinions or responses.
3. Everyday Life:
- Tipping: Calculating tips in restaurants often involves expressing the tip as a percentage of the bill.
- Grade Calculations: Grades in schools are frequently expressed as percentages.
- Sales and Promotions: Understanding percentages is essential to take advantage of sales and promotions.
- Cooking and Baking: Many recipes use percentages to indicate the proportion of ingredients.
Beyond the Basics: Advanced Percentage Concepts
While calculating "what percent is 22 of 40" is straightforward, percentage calculations can become more complex. Here are some advanced concepts:
1. Percentage Increase and Decrease:
These calculations involve determining the percentage change between two values. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] * 100%
Similarly, the formula for percentage decrease is:
[(Old Value - New Value) / Old Value] * 100%
2. Percentage Points:
It's crucial to distinguish between percentage points and percentage changes. For example, a change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
3. Percentage of a Percentage:
This involves calculating a percentage of a percentage, requiring multiple percentage calculations. For example, finding 15% of 20% of 500 involves two steps: finding 20% of 500 (100), then finding 15% of 100 (15).
Practicing Percentage Calculations
Mastering percentage calculations requires practice. Try solving various percentage problems to build your skills and confidence. Start with simple problems and gradually increase the complexity. Use different methods to solve the same problem to reinforce your understanding.
Conclusion
Calculating "what percent is 22 of 40" – which we've established is 55% – is a fundamental skill with wide-ranging applications. Understanding percentages is vital for various aspects of life, from personal finance to professional fields. By mastering the different methods for calculating percentages and understanding the underlying concepts, you'll be equipped to handle more complex calculations and confidently navigate situations involving proportions and ratios. The ability to perform percentage calculations accurately and efficiently is a valuable asset in the modern world.
Latest Posts
Latest Posts
-
How Do You Know If A Chemical Reaction Has Occurred
Apr 26, 2025
-
Cuanto Es 1 63 Cm En Pies
Apr 26, 2025
-
How Many Inches Is 19 5 Cm
Apr 26, 2025
-
How Many Acute Angles Does An Obtuse Triangle Have
Apr 26, 2025
-
160 Cm A Pies Y Pulgadas
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 22 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.