What Percent Is 23 Of 30
Kalali
Apr 23, 2025 · 5 min read
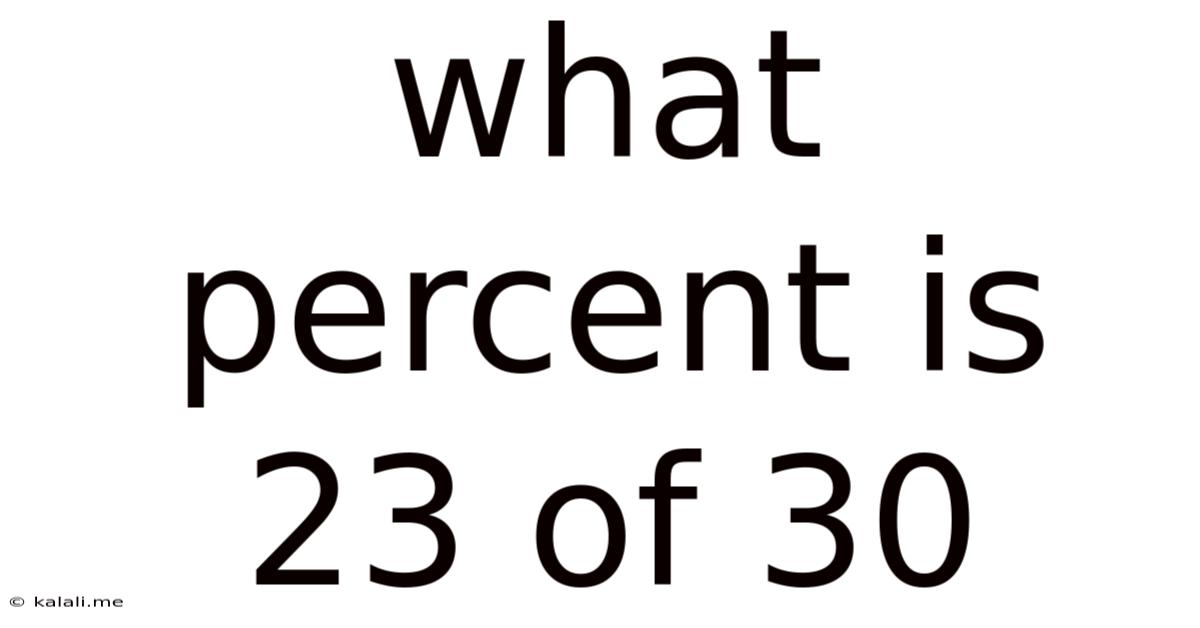
Table of Contents
What Percent is 23 of 30? A Deep Dive into Percentage Calculations and Real-World Applications
What percent is 23 of 30? This seemingly simple question opens the door to a world of percentage calculations, their applications, and the underlying mathematical principles. While the answer itself is straightforward, understanding the how and why behind the calculation is crucial for numerous real-world scenarios, from calculating grades to understanding financial data. This article will not only answer the initial question but also explore various methods of calculating percentages, common applications, and advanced techniques for handling percentage-related problems.
Meta Description: Discover how to calculate what percent 23 is of 30. This comprehensive guide explores various percentage calculation methods, real-world applications, and advanced techniques, providing a thorough understanding of this fundamental mathematical concept.
The Basic Calculation: Finding the Percentage
The most fundamental method to determine what percent 23 is of 30 involves using a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
(23 / 30) * 100% = 76.67%
Therefore, 23 is approximately 76.67% of 30. The slight decimal remainder highlights the importance of understanding how to round percentages appropriately depending on the context. For instance, in a grading system, you might round to the nearest whole number, while in financial calculations, more decimal places might be necessary for accuracy.
Alternative Methods for Calculating Percentages
While the above method is the most direct, several alternative approaches can be used, depending on your preference and the complexity of the problem:
-
Using Proportions: This method sets up a proportion where x/100 represents the unknown percentage:
23/30 = x/100
Cross-multiplying gives:
30x = 2300
Solving for x:
x = 2300/30 = 76.67
-
Using Decimal Conversion: First, convert the fraction 23/30 into a decimal by performing the division: 23 ÷ 30 ≈ 0.7667. Then, multiply the decimal by 100% to express it as a percentage: 0.7667 * 100% = 76.67%.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 23 ÷ 30 = and then multiply by 100. Some calculators allow you to directly input the calculation as (23/30)*100%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital across many aspects of daily life:
-
Academic Performance: Calculating grades often involves determining the percentage of correct answers or the weighted average of different assignment scores. For example, if a student scores 23 out of 30 on a test, their percentage score is 76.67%, as calculated above.
-
Financial Matters: Percentages are fundamental in finance. Calculating interest rates, discounts, tax rates, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage change is also crucial for tracking financial performance over time. For example, a 10% increase in salary or a 5% decrease in the value of an investment can be easily calculated using percentage formulas.
-
Sales and Marketing: Discounts are often expressed as percentages (e.g., a 20% off sale). Calculating the final price after a discount involves subtracting the percentage discount from the original price. Similarly, commission calculations for sales representatives are often based on a percentage of sales revenue. Analyzing market share also relies on percentages.
-
Data Analysis and Statistics: Percentages are extensively used in representing data and statistics, allowing for easy comparison and visualization. For example, survey results, demographic data, and scientific studies frequently utilize percentages to convey findings efficiently. Understanding percentage points is also crucial when comparing percentage changes. A shift from 20% to 30% is a 10 percentage point increase, not a 50% increase.
-
Everyday Life: Percentages are used in many other everyday situations. For example, calculating tips at restaurants, determining the percentage of ingredients in a recipe, understanding nutritional information on food labels, and even interpreting weather forecasts often involves percentage calculations.
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond the basic calculation, understanding percentage increases and decreases is essential.
-
Percentage Increase: This calculates the percentage change when a value increases. The formula is:
[(New Value - Old Value) / Old Value] * 100%For example, if a product's price increases from $30 to $35, the percentage increase is:
[(35 - 30) / 30] * 100% = 16.67% -
Percentage Decrease: This calculates the percentage change when a value decreases. The formula is:
[(Old Value - New Value) / Old Value] * 100%For example, if a product's price decreases from $30 to $25, the percentage decrease is:
[(30 - 25) / 30] * 100% = 16.67%
Working with Multiple Percentages
Sometimes, you need to work with multiple percentages in a single calculation. For instance, calculating the final price after applying multiple discounts requires careful consideration of the order of operations. Applying a 10% discount followed by a 20% discount does not result in a 30% discount. The discounts are applied sequentially.
Troubleshooting Common Percentage Calculation Errors
Common mistakes when calculating percentages include:
-
Incorrect Order of Operations: Remember the order of operations (PEMDAS/BODMAS). Parentheses, exponents, multiplication and division (from left to right), addition and subtraction (from left to right).
-
Confusing Percentage Points and Percentage Change: Remember the distinction between percentage points and percentage changes.
-
Rounding Errors: Rounding too early in the calculation can lead to significant inaccuracies in the final result. It's best to round only at the very end.
-
Incorrect Formula Application: Ensure you are using the correct formula for the specific type of percentage calculation you are performing.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate what percent 23 is of 30, and more generally, mastering percentage calculations, is a fundamental skill applicable across numerous fields. From academic assessments to financial planning and data analysis, the ability to work confidently with percentages is crucial for making informed decisions and interpreting information effectively. By mastering the basic formula and its various applications, you equip yourself with a valuable tool for navigating a wide range of quantitative situations. Remember to practice regularly and pay close attention to detail to avoid common errors, ultimately improving accuracy and confidence in your percentage calculations. This comprehensive understanding ensures you're not just finding the answer, but deeply understanding the underlying mathematical concept and its widespread relevance.
Latest Posts
Latest Posts
-
How Many Ounces Is 8 Pounds
Apr 23, 2025
-
What Is 2 75 In Fraction Form
Apr 23, 2025
-
1000 Ml Is Equal To How Many Liters
Apr 23, 2025
-
Can A Human Be Cold Blooded
Apr 23, 2025
-
Does Magnesium And Oxygen Form An Ionic Compound
Apr 23, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 23 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.