What Percent Is 3 Of 7
Kalali
Apr 18, 2025 · 5 min read
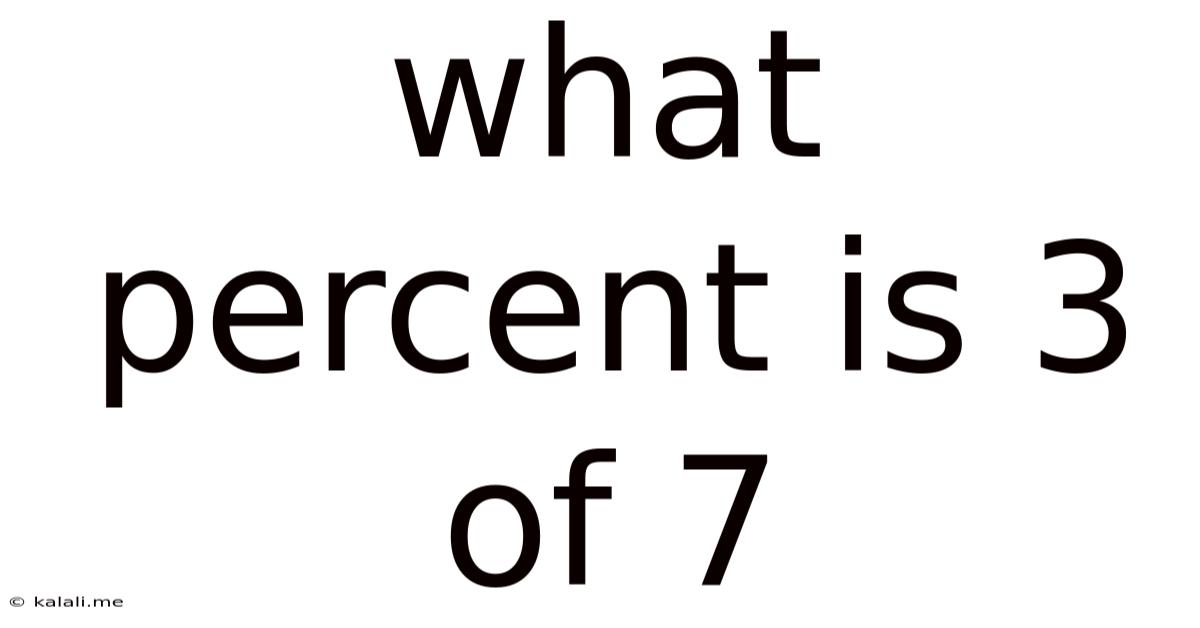
Table of Contents
What Percent is 3 of 7? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent is 3 of 7?", opens the door to a deeper understanding of percentages, their applications, and how to effectively calculate them. This article will not only answer the question directly but also explore various methods for calculating percentages, delve into the practical applications of percentage calculations, and offer helpful tips for improving your understanding and skills in this crucial mathematical area. Understanding percentages is fundamental to numerous aspects of life, from financial planning and budgeting to interpreting data and understanding statistics.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to find what percent 3 is of 7. This guide covers various methods, real-world applications, and tips to master percentage calculations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred". The symbol % is used to denote percentages. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are used to represent proportions or parts of a whole. They provide a standardized way to compare different quantities and make data easier to understand. For instance, if a student scores 85% on a test, it means they answered 85 out of 100 questions correctly. Similarly, if a store offers a 20% discount, it means you'll pay 20% less than the original price.
Calculating "What Percent is 3 of 7?"
Now, let's address the core question: What percent is 3 of 7? We can solve this using several methods:
Method 1: Using the Proportion Method
This method is based on setting up a proportion:
- Part/Whole = Percentage/100
In our case:
- Part = 3
- Whole = 7
- Percentage = x (what we need to find)
Substituting these values into the proportion, we get:
- 3/7 = x/100
To solve for x, we cross-multiply:
- 3 * 100 = 7 * x
- 300 = 7x
- x = 300/7
- x ≈ 42.86
Therefore, 3 is approximately 42.86% of 7.
Method 2: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
- Convert the fraction to a decimal: 3/7 ≈ 0.4286
- Multiply the decimal by 100: 0.4286 * 100 = 42.86%
This confirms our result from the proportion method.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide 3 by 7 and then multiply the result by 100. This provides a quick and accurate way to calculate the percentage.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in many real-world situations. Here are a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentage calculations. Understanding compound interest, for instance, requires a solid grasp of percentage growth. Budgeting and financial planning also rely heavily on percentages to track expenses and savings.
-
Sales and Marketing: Analyzing sales data, calculating conversion rates, and determining the effectiveness of marketing campaigns often involves percentage calculations. Understanding market share, customer acquisition costs, and return on investment (ROI) all require proficiency in percentage calculations.
-
Data Analysis and Statistics: Percentages are widely used to present data clearly and concisely. They help to express proportions, compare different groups, and identify trends. Understanding statistical concepts like percentiles and standard deviation often requires working with percentages.
-
Science and Engineering: Percentages are used to express concentrations of solutions, efficiencies of machines, and error rates in experiments. In fields like chemistry, calculating the percentage composition of elements in a compound is a standard practice.
-
Everyday Life: Calculating tips in restaurants, understanding discounts in stores, figuring out the percentage of ingredients in a recipe, and even interpreting weather forecasts (e.g., a 30% chance of rain) all involve percentages.
Improving Your Percentage Calculation Skills
Here are some tips to improve your skills in calculating percentages:
-
Master the basics: Ensure you have a solid understanding of fractions, decimals, and ratios. These concepts are fundamental to working with percentages.
-
Practice regularly: The more you practice, the more comfortable and efficient you'll become. Try solving various percentage problems from different contexts.
-
Use different methods: Experiment with various methods for calculating percentages (proportion, decimal conversion, calculator) to find the approach that works best for you.
-
Check your work: Always double-check your calculations to ensure accuracy. Use estimation to verify the reasonableness of your answers.
-
Utilize online resources: There are numerous online calculators and tutorials available to help you practice and improve your skills. Explore interactive exercises and quizzes to reinforce your learning.
-
Relate percentages to real-world scenarios: Try applying percentage calculations to real-life situations to enhance your understanding and improve retention.
Beyond the Basics: More Complex Percentage Problems
While "What percent is 3 of 7?" is a straightforward problem, percentage calculations can become more complex. For example, you might encounter problems involving:
-
Percentage increase or decrease: Calculating the percentage change between two values. For example, what is the percentage increase from 10 to 15? This involves finding the difference (5), dividing it by the original value (10), and multiplying by 100 (50%).
-
Percentage points: This is a common source of confusion. Percentage points represent the absolute difference between two percentages. For instance, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Compound percentages: These involve calculating percentages of percentages, often used in scenarios like compound interest or population growth. Understanding how compound interest works is crucial for long-term financial planning.
-
Successive percentages: Calculating the overall percentage change when multiple percentage changes are applied sequentially. For example, a 10% increase followed by a 20% decrease will not result in a net 10% decrease.
Mastering these more advanced percentage calculations requires a strong foundation in the basics and a willingness to practice diverse problem types.
Conclusion: The Importance of Percentage Proficiency
The ability to calculate percentages is a fundamental skill applicable across numerous fields. While the question "What percent is 3 of 7?" may seem simple, it serves as a gateway to understanding the broader world of percentage calculations and their significant role in our lives. By mastering the techniques discussed in this article and practicing regularly, you can significantly enhance your quantitative skills and improve your ability to interpret and analyze data effectively. Remember, proficiency in percentages is not just about numbers; it's about understanding proportions, interpreting data, and making informed decisions in various aspects of your life.
Latest Posts
Latest Posts
-
What Is 20 Off Of 70
Apr 19, 2025
-
25 Is What Percent Of 65
Apr 19, 2025
-
How Many Ounces In 2 1 2 Quarts
Apr 19, 2025
-
17 Is What Percent Of 68
Apr 19, 2025
-
How Big Is 36 Inches In Feet
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 3 Of 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.