What Percent Is 3 Of 8
Kalali
Apr 15, 2025 · 5 min read
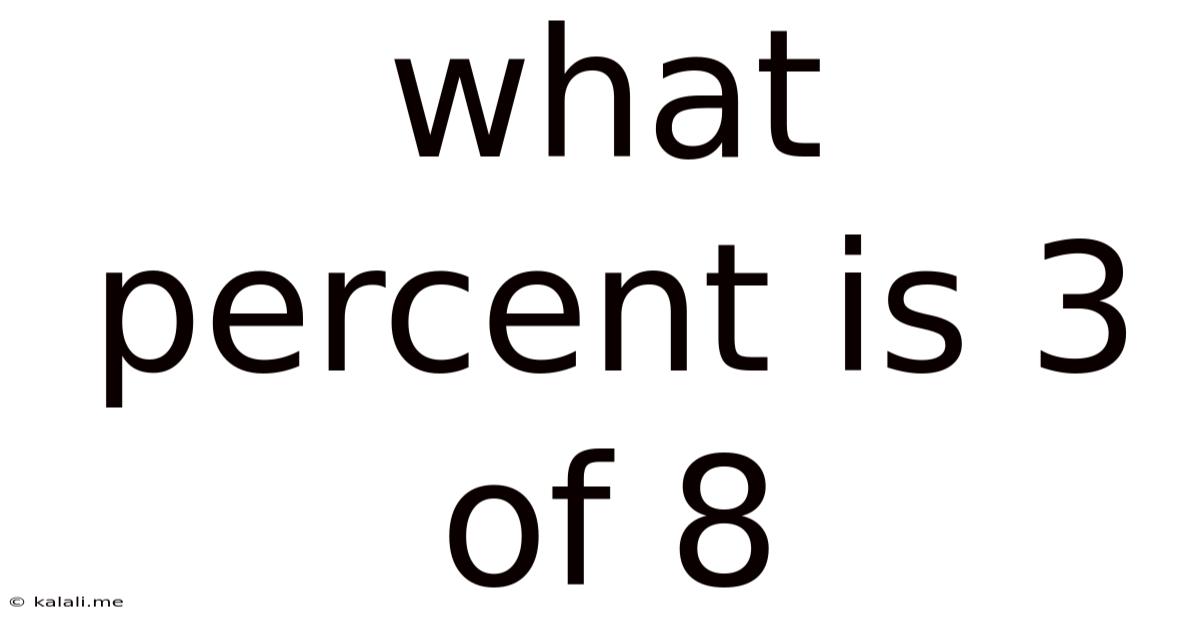
Table of Contents
What Percent is 3 of 8? A Deep Dive into Percentage Calculations
This seemingly simple question – "What percent is 3 of 8?" – opens the door to a broader understanding of percentage calculations, their applications, and the underlying mathematical principles. While the answer itself is straightforward, exploring the various methods and contexts in which this type of calculation is used provides valuable insights for students, professionals, and anyone seeking to improve their numerical literacy. This article will not only answer the question directly but also delve into the different approaches to solving percentage problems, explore real-world applications, and discuss common misconceptions.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to determine what percent 3 is of 8. We cover various methods, real-world applications, and common mistakes to avoid. Master percentage calculations with this comprehensive guide.
Understanding the Fundamentals of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5. Percentages are used extensively in various fields, from finance and statistics to everyday life, making them an essential concept to grasp.
Method 1: The Direct Proportion Method
The most straightforward way to determine what percent 3 is of 8 is using a direct proportion. We can set up the equation as follows:
- 3/8 = x/100
Where 'x' represents the percentage we are trying to find. To solve for x, we cross-multiply:
- 8x = 300
Then, divide both sides by 8:
- x = 300/8 = 37.5
Therefore, 3 is 37.5% of 8.
Method 2: Using Decimal Conversion
This method involves first converting the fraction 3/8 into a decimal. We divide 3 by 8:
- 3 ÷ 8 = 0.375
To convert this decimal to a percentage, we multiply by 100:
- 0.375 x 100 = 37.5%
This method is particularly useful when dealing with more complex fractions or when using a calculator.
Method 3: The Percentage Formula
The general formula for calculating percentages is:
- (Part / Whole) x 100 = Percentage
In our case:
- (3 / 8) x 100 = 37.5%
This formula is a versatile tool applicable to a wide range of percentage problems. Understanding this formula allows for easier adaptation to various scenarios.
Real-World Applications: Where Percentage Calculations Matter
The ability to calculate percentages is crucial in various aspects of life. Here are a few examples:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and returns on investment all rely heavily on percentage calculations. Understanding percentage changes is vital for tracking financial performance. For example, if a stock price increases from $8 to $11, the percentage increase is calculated as (($11-$8)/$8) x 100% = 37.5%.
-
Statistics: Percentages are fundamental in interpreting statistical data. Surveys, polls, and research studies often present results in percentages to make them easier to understand and compare. For instance, if a survey of 800 people shows that 300 prefer a particular brand, the percentage of people preferring that brand is (300/800) x 100% = 37.5%.
-
Shopping: Discounts and sales are often expressed as percentages. Calculating the final price after a discount requires understanding percentage reductions. If an item is priced at $8 and is discounted by 37.5%, the discount amount is $8 x 0.375 = $3, and the final price is $8 - $3 = $5.
-
Science: Percentage calculations are commonly used in scientific studies to represent data, such as the percentage composition of elements in a compound or the percentage change in a measured variable.
-
Everyday Life: From calculating tips in restaurants (e.g., a 15% tip on an $8 meal) to understanding nutritional information on food labels (e.g., the percentage of daily recommended values), percentages are integral to our daily routines.
Common Mistakes to Avoid
Several common errors can lead to inaccurate percentage calculations. These include:
-
Incorrect Order of Operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps. Incorrect sequencing can lead to significant errors.
-
Confusing Part and Whole: Clearly identify the "part" and the "whole" in the problem before applying the formula. Mistaking one for the other will result in an incorrect answer.
-
Incorrect Decimal to Percentage Conversion: Remember to multiply the decimal by 100 to convert it to a percentage. Forgetting this step is a frequent error.
-
Rounding Errors: Rounding off numbers too early in the calculation can lead to accumulating errors, especially when dealing with multiple steps. It's best to wait until the final step to round off the answer to the desired level of precision.
-
Using the Wrong Formula: Ensure you are using the appropriate percentage formula for the specific problem. There are different formulas for calculating percentage increases, decreases, and changes.
Expanding the Concept: Percentage Increase and Decrease
While the initial question focused on a simple percentage calculation, it's beneficial to expand on the concept to include percentage increases and decreases. These calculations involve determining the percentage change between two values.
Percentage Increase: If a value increases from an initial value to a final value, the percentage increase is calculated as:
- [(Final Value - Initial Value) / Initial Value] x 100%
Percentage Decrease: If a value decreases from an initial value to a final value, the percentage decrease is calculated as:
- [(Initial Value - Final Value) / Initial Value] x 100%
For example, if a value increases from 8 to 11, the percentage increase is [(11-8)/8] x 100% = 37.5%. If it decreases from 8 to 5, the percentage decrease is [(8-5)/8] x 100% = 37.5%.
Advanced Applications: Compound Interest and Growth Rates
Percentage calculations form the foundation for understanding compound interest and growth rates, crucial concepts in finance and economics. Compound interest involves earning interest on both the principal amount and accumulated interest. Growth rates, whether in population, economies, or investments, are often expressed as percentages to illustrate the rate of change over time.
Conclusion: Mastering Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields. This article has explored various methods for calculating percentages, focusing specifically on determining what percent 3 is of 8 (37.5%), and highlighted their real-world applications. By avoiding common mistakes and understanding the underlying principles, one can confidently tackle a wide range of percentage problems, from simple calculations to more complex scenarios involving compound interest and growth rates. Mastering percentage calculations significantly enhances numerical literacy and problem-solving abilities, making it a valuable skill for both personal and professional success.
Latest Posts
Latest Posts
-
What Is Sublimation In The Water Cycle
Apr 16, 2025
-
In Celsius What Is The Freezing Point Of Water
Apr 16, 2025
-
52 In Is How Many Feet
Apr 16, 2025
-
Cuanto Son 10 Cm En Pulgadas
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 3 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.