What Percent Is 3 Out Of 4
Kalali
Apr 11, 2025 · 5 min read
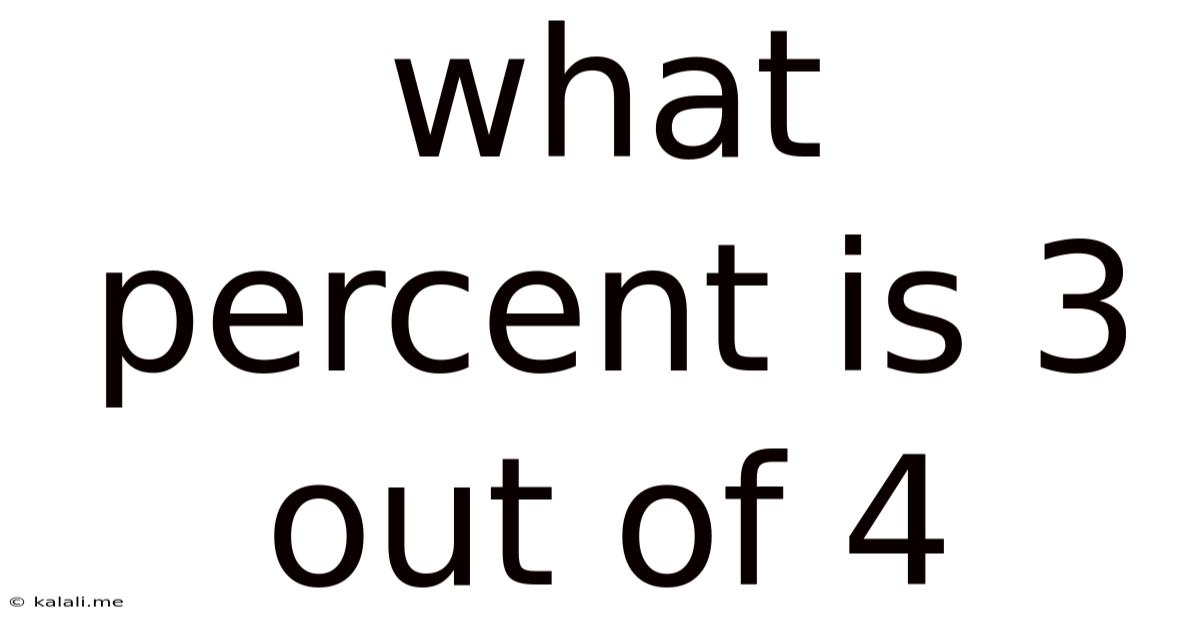
Table of Contents
What Percent is 3 out of 4? A Deep Dive into Percentages and Their Applications
What percent is 3 out of 4? The answer, at its simplest, is 75%. But this seemingly straightforward question opens the door to a broader understanding of percentages, their calculation, and their widespread applications in various fields. This article delves into the intricacies of calculating percentages, exploring different methods and providing practical examples to solidify your comprehension. We'll also examine the significance of understanding percentages in everyday life and professional settings.
Meta Description: Learn how to calculate percentages effortlessly! This comprehensive guide explains how to determine what percent 3 out of 4 represents, covering different methods, real-world applications, and the importance of percentage calculations in various fields.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ("per cent" in Latin). Therefore, 75% means 75 out of 100, or 75/100. Understanding this fundamental concept is crucial for grasping percentage calculations.
We can represent this visually: imagine a pie chart divided into 100 equal slices. 75% would represent 75 of those slices. Similarly, 3 out of 4 represents three-quarters of a whole. To convert this fraction to a percentage, we need to find an equivalent fraction with a denominator of 100.
Calculating "What Percent is 3 out of 4?" – Method 1: Using Fractions
The most straightforward method involves converting the fraction 3/4 into a percentage. Here's the step-by-step process:
-
Set up the fraction: We begin with the given fraction, 3/4.
-
Convert to a decimal: Divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.75 x 100 = 75%
Therefore, 3 out of 4 is equivalent to 75%.
Calculating "What Percent is 3 out of 4?" – Method 2: Using Proportions
Another approach involves setting up a proportion. This method is particularly useful when dealing with more complex percentage problems.
-
Set up the proportion: We set up a proportion where x represents the unknown percentage:
3/4 = x/100
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa:
4x = 300
-
Solve for x: Divide both sides of the equation by 4:
x = 300 ÷ 4 = 75
Therefore, x = 75%, confirming that 3 out of 4 is 75%.
Real-World Applications of Percentage Calculations
Understanding percentages is vital in numerous aspects of daily life and professional fields. Here are just a few examples:
-
Sales and Discounts: Retail stores frequently advertise discounts as percentages. For example, a "25% off" sale means you pay 75% of the original price.
-
Finance and Investing: Interest rates, returns on investments, and loan calculations all involve percentages. Understanding compound interest, for instance, requires a solid grasp of percentage calculations.
-
Statistics and Data Analysis: Percentages are essential for interpreting data and drawing conclusions from surveys, polls, and research studies. Representing data using percentages provides a clear and concise way to visualize proportions.
-
Taxes: Income tax, sales tax, and property tax are all calculated as percentages of your income or the value of a property.
-
Grade Calculations: In many educational systems, final grades are expressed as percentages representing the student's performance relative to the total possible points.
-
Health and Medicine: Doctors often express the effectiveness of treatments or the prevalence of diseases using percentages. For example, a vaccine's effectiveness might be described as 95% effective.
Beyond the Basics: More Complex Percentage Problems
While "What percent is 3 out of 4?" is a relatively simple problem, the principles involved can be applied to more complex scenarios. Let's explore some variations:
-
Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. For example, if a stock price increases from $10 to $12, the percentage increase is calculated as follows:
-
Find the difference: $12 - $10 = $2
-
Divide the difference by the original value: $2 / $10 = 0.2
-
Convert to a percentage: 0.2 x 100 = 20%
Therefore, the stock price increased by 20%.
-
-
Finding a Percentage of a Number: This involves calculating a certain percentage of a given value. For example, finding 15% of 200:
-
Convert the percentage to a decimal: 15% = 0.15
-
Multiply the decimal by the number: 0.15 x 200 = 30
Therefore, 15% of 200 is 30.
-
-
Finding the Original Value After a Percentage Change: This involves working backwards from a percentage change to find the original value. For example, if a price increased by 10% to $110, the original price can be calculated as follows:
-
Recognize that the final price represents 110% of the original price.
-
Set up an equation: 1.10x = $110 (where x is the original price)
-
Solve for x: x = $110 / 1.10 = $100
Therefore, the original price was $100.
-
Practical Tips for Mastering Percentage Calculations
-
Practice Regularly: The key to mastering percentages is consistent practice. Work through various problems of increasing complexity to build your understanding.
-
Use a Calculator: While mental calculations are helpful, using a calculator can save time and ensure accuracy, especially with more complex problems.
-
Understand the Concepts: Don't just memorize formulas; strive to understand the underlying concepts. This will enable you to apply the principles to different situations.
-
Visualize the Problem: Using visual aids like pie charts or diagrams can help you visualize the problem and understand the relationships between values.
-
Break Down Complex Problems: When faced with a complex percentage problem, break it down into smaller, more manageable steps.
Conclusion: The Importance of Percentage Literacy
Understanding percentages is a fundamental skill applicable across numerous disciplines. From everyday shopping to complex financial decisions, the ability to calculate and interpret percentages empowers you to make informed choices and navigate the world with greater confidence. While the simple question "What percent is 3 out of 4?" provides a starting point, this article highlights the broader significance of percentage literacy and provides the tools and methods to tackle more intricate percentage calculations with ease. Mastering this skill significantly enhances your numerical fluency and opens doors to a deeper understanding of the quantitative world around us. By practicing the methods outlined and applying them to real-world scenarios, you'll solidify your understanding of percentages and their significant role in various aspects of life.
Latest Posts
Latest Posts
-
How Many Centimeters In 6 Meters
Apr 18, 2025
-
What Are The Factors For 2
Apr 18, 2025
-
Is Malleable A Chemical Or Physical Property
Apr 18, 2025
-
25 Cm Is Equal To How Many Inches
Apr 18, 2025
-
What Percentage Is 20 Out Of 25
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 3 Out Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.