What Percent Is 35 Of 50
Kalali
Apr 08, 2025 · 5 min read
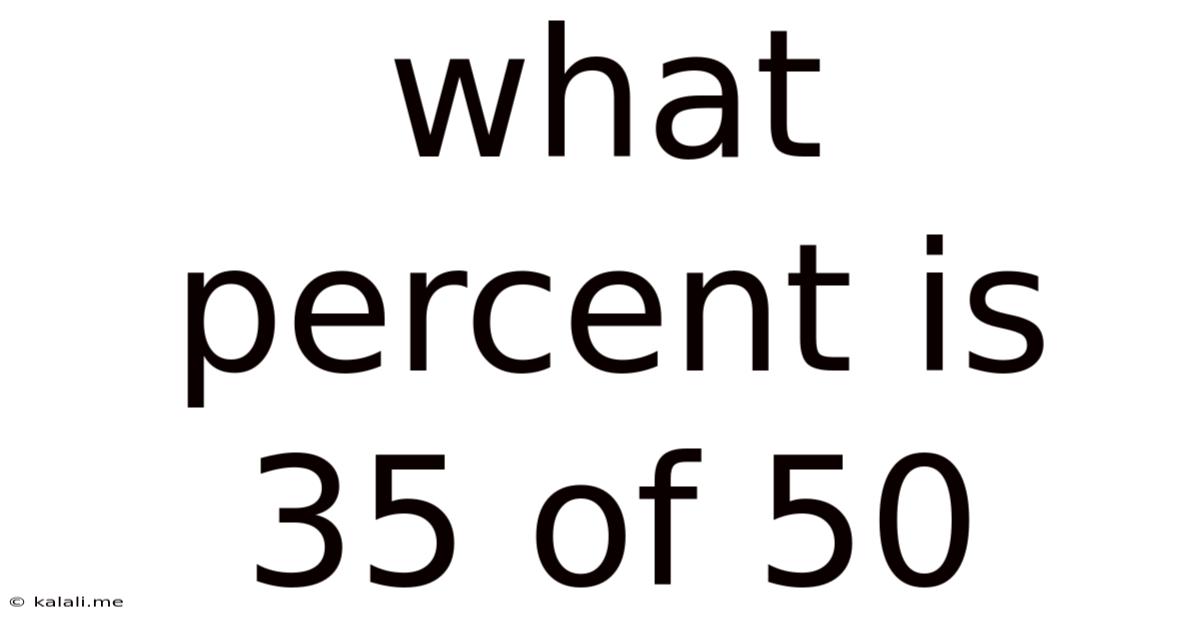
Table of Contents
What Percent is 35 of 50? A Deep Dive into Percentage Calculations and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will thoroughly explore the question "What percent is 35 of 50?", providing not just the answer but a comprehensive understanding of the underlying principles and practical applications of percentage calculations. We'll cover different methods for solving percentage problems, discuss common errors to avoid, and delve into real-world examples demonstrating the usefulness of this mathematical concept. Understanding percentages is crucial for informed decision-making and navigating the numerical world effectively.
Understanding Percentages: The Fundamentals
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, 50% means 50 out of 100, which can also be expressed as the fraction 50/100 or the decimal 0.5.
The fundamental formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our specific problem, "What percent is 35 of 50?", 35 represents the "part" and 50 represents the "whole." Let's apply the formula:
(35 / 50) * 100% = 70%
Therefore, 35 is 70% of 50.
Methods for Calculating Percentages
While the basic formula is straightforward, there are several approaches to solving percentage problems, each offering varying levels of efficiency and suitability depending on the context:
-
Using the Formula Directly: This is the most fundamental method, directly substituting the values into the formula (Part / Whole) * 100%. This method works well for simple calculations.
-
Simplifying the Fraction: Before multiplying by 100%, simplifying the fraction (Part / Whole) can make the calculation easier. In our example, 35/50 can be simplified to 7/10. Multiplying 7/10 by 100% gives 70%. This method is beneficial for mental calculations or when dealing with larger numbers.
-
Using Proportions: This method involves setting up a proportion: Part / Whole = Percentage / 100. Cross-multiplying and solving for the unknown percentage provides the answer. This method can be particularly helpful for solving more complex percentage problems. For our example:
35 / 50 = x / 100
50x = 3500
x = 70
-
Using Decimal Equivalents: Converting the fraction to a decimal and then multiplying by 100% also works effectively. 35/50 = 0.7. Multiplying 0.7 by 100% results in 70%.
Common Mistakes to Avoid When Calculating Percentages
Several common mistakes can lead to inaccurate percentage calculations:
-
Incorrect Order of Operations: Always perform the division (Part / Whole) before multiplying by 100%. Failing to follow the order of operations can yield incorrect results.
-
Misinterpreting the Question: Carefully read and understand the problem statement. Identify the "part" and the "whole" correctly to avoid errors. Often, the wording can be subtly misleading.
-
Rounding Errors: When dealing with decimal values, be mindful of rounding errors. Rounding prematurely can significantly affect the final result. Ideally, retain as many decimal places as possible throughout the calculation before rounding the final answer.
-
Unit Confusion: Ensure consistent units throughout the calculation. If dealing with percentages related to currency, weight, or volume, make sure all measurements are in the same units.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various fields:
-
Finance: Calculating interest rates, loan payments, discounts, taxes, profit margins, and investment returns. Understanding percentages is fundamental to financial literacy.
-
Business: Analyzing sales figures, market share, profit and loss statements, and assessing the effectiveness of marketing campaigns. Businesses heavily rely on percentage calculations for decision-making.
-
Science: Expressing experimental data, calculating error margins, and representing statistical probabilities. Percentages are crucial for data analysis and interpretation.
-
Everyday Life: Calculating tips in restaurants, understanding discounts in stores, interpreting nutritional information on food labels, and calculating grades in school. Percentages are integral to daily decision-making.
-
Data Analysis: Presenting data in a clear and concise manner. Percentages allow easy comparison of different datasets. For example, comparing the percentage of men versus women in a particular profession.
Advanced Percentage Problems and Concepts
Beyond the basic calculation, several advanced percentage problems and concepts warrant exploration:
-
Percentage Increase/Decrease: Calculating the percentage change between two values. This involves finding the difference between the two values, dividing by the original value, and multiplying by 100%.
-
Percentage Points: A percentage point represents the difference between two percentages. For example, a change from 10% to 15% is a 5-percentage point increase, not a 50% increase.
-
Compound Interest: Interest earned on both the principal amount and accumulated interest. This concept is crucial in understanding long-term investments and loan repayments.
-
Percentage of a Percentage: Calculating a percentage of a percentage involves multiplying the two percentages together (after converting them to decimal form). For example, finding 20% of 50% is equivalent to 0.2 * 0.5 = 0.1, or 10%.
Conclusion: Mastering Percentage Calculations for Success
Understanding percentages is a critical life skill applicable across numerous domains. By mastering the fundamental formula and different calculation methods, while avoiding common pitfalls, individuals can confidently handle percentage problems in various contexts. From navigating everyday financial transactions to analyzing complex datasets, the ability to calculate and interpret percentages is essential for informed decision-making and achieving success in both personal and professional endeavors. The simple calculation of "What percent is 35 of 50?" serves as a gateway to understanding this powerful mathematical tool and its vast practical applications. Proficiency in percentage calculations equips individuals with a valuable skill set for navigating the quantitative aspects of modern life.
Latest Posts
Latest Posts
-
What Is A 22 Out Of 26
Apr 17, 2025
-
Cuanto Es 17 Centimetros En Pulgadas
Apr 17, 2025
-
How Many Pints In 2 Gallons
Apr 17, 2025
-
How Many Hours Is 111 Minutes
Apr 17, 2025
-
How Much Is 1 3 Of A Pound
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 35 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.