What Percent Is 38 Of 40
Kalali
Apr 16, 2025 · 5 min read
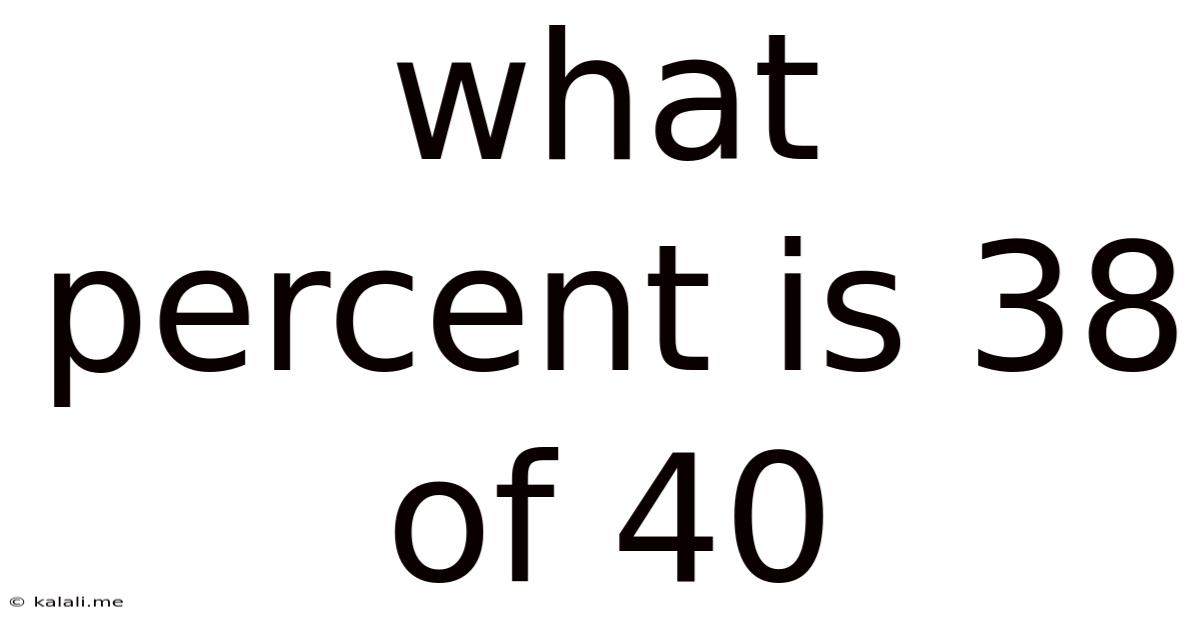
Table of Contents
What Percent is 38 of 40? A Deep Dive into Percentage Calculations and Applications
What percent is 38 of 40? At first glance, this seems like a simple question with a straightforward answer. However, understanding how to calculate this percentage, and more importantly, grasping the underlying concepts and applications, reveals a fundamental skill crucial across numerous fields, from everyday budgeting to complex financial modeling. This article will not only provide the solution but delve into the methodology, explore various calculation methods, and discuss real-world applications of percentage calculations.
Meta Description: Discover how to calculate what percent 38 is of 40. This in-depth guide explores different methods, explains the underlying concepts, and reveals real-world applications of percentage calculations, making you a percentage pro!
Understanding Percentages: The Basics
Before jumping into the calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per hundred" or "out of 100." Therefore, 50% represents 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Understanding this foundation is key to solving percentage problems. We're essentially asking: if 40 represents the whole (100%), what percentage does 38 represent?
Method 1: The Proportion Method
This method uses a proportion to solve the problem. We set up a proportion where one ratio represents the known values (38 out of 40), and the other ratio uses 'x' to represent the unknown percentage (x out of 100).
-
Set up the proportion: 38/40 = x/100
-
Cross-multiply: 40x = 3800
-
Solve for x: x = 3800 / 40 = 95
-
Therefore: 38 is 95% of 40.
Method 2: The Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
-
Convert the fraction: 38/40 = 0.95
-
Multiply by 100: 0.95 * 100 = 95
-
Therefore: 38 is 95% of 40.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide 38 by 40 and then multiply the result by 100. The answer will be 95%. This method is particularly useful for more complex percentage calculations.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is invaluable in numerous real-world scenarios. Here are a few examples:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all heavily rely on percentage calculations. For example, understanding that a 20% discount on a $100 item saves you $20 is a direct application of percentage calculations. Similarly, understanding compound interest requires a strong grasp of percentage growth over time.
-
Statistics and Data Analysis: Percentages are used extensively in presenting and interpreting data. For instance, analyzing survey results, expressing market share, or representing growth rates often requires converting raw data into percentages for easier understanding and comparison. A company might report that 95% of its customers are satisfied, demonstrating the use of percentages in customer satisfaction surveys.
-
Science: Percentage calculations are fundamental in many scientific disciplines, such as chemistry (concentration of solutions), biology (population growth), and physics (efficiency of energy conversion). For example, the concentration of a chemical solution might be expressed as a percentage, such as a 10% saline solution.
-
Everyday Life: From calculating tips at restaurants (calculating 15% or 20% of the bill) to understanding sales tax (calculating 6% or 7% on purchases) percentages are woven into our daily routines. Even determining the percentage of tasks completed in a project relies on percentage calculations.
-
Education: Grading systems, test scores, and overall academic performance are often expressed as percentages. Understanding your percentage score on an exam is a direct application of percentage calculations. The concept of a weighted average (where different aspects of a grade contribute different percentages to the overall mark) also heavily relies on percentage calculations.
-
Business: Businesses utilize percentage calculations for everything from cost analysis (determining the percentage of overall cost attributable to specific elements like materials or labor) to profit margins and return on investment (ROI). A company might aim for a 15% profit margin, highlighting the significant role of percentage targets in business strategy.
Beyond the Basics: More Complex Percentage Problems
While the initial problem was relatively straightforward, percentage calculations can become significantly more complex. Here are a few examples of more advanced problems:
-
Finding the original value: If a discounted item costs $80 after a 20% discount, what was the original price?
-
Finding the percentage increase or decrease: If a quantity increases from 50 to 60, what is the percentage increase?
-
Compound percentages: Calculating the total value after applying multiple percentage changes sequentially (e.g., a 10% increase followed by a 5% decrease).
-
Percentage points: Understanding the difference between a percentage change and percentage points (e.g., an increase from 10% to 15% is a 5 percentage point increase, but a 50% percentage increase).
Solving these more complex problems requires a more profound understanding of algebraic manipulation and the interplay between percentages, fractions, and decimals.
Developing Strong Percentage Skills
Mastering percentage calculations is a journey, not a destination. Consistent practice and a clear understanding of the underlying concepts are key to building proficiency. Here are some tips to enhance your skills:
-
Practice regularly: Solve a variety of percentage problems, starting with simpler ones and gradually progressing to more complex scenarios.
-
Visualize the problem: Drawing diagrams or using visual aids can help you understand the relationships between different values.
-
Break down complex problems: Divide complex problems into smaller, manageable steps.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Utilize online resources: There are many online resources, tutorials, and practice exercises available to help you hone your percentage calculation skills.
Conclusion
The answer to "What percent is 38 of 40?" is 95%. However, this simple question unveils a world of applications for percentage calculations. From navigating everyday finances to analyzing complex datasets, a firm grasp of percentages is crucial for success in various aspects of life. By understanding the different methods for calculating percentages and practicing regularly, you can build confidence and proficiency in this essential mathematical skill. Remember, the key is not just knowing the answer, but understanding the process and its far-reaching relevance.
Latest Posts
Latest Posts
-
How Many Hours Is 285 Minutes
Apr 19, 2025
-
How Many Species Of Reptiles Are There
Apr 19, 2025
-
6 Cups Equals How Many Pints
Apr 19, 2025
-
How To Do Mole To Mass Conversions
Apr 19, 2025
-
Life Cycle Of A Plant Bean
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 38 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.