What Percent Is 5 Out Of 20
Kalali
Apr 09, 2025 · 5 min read
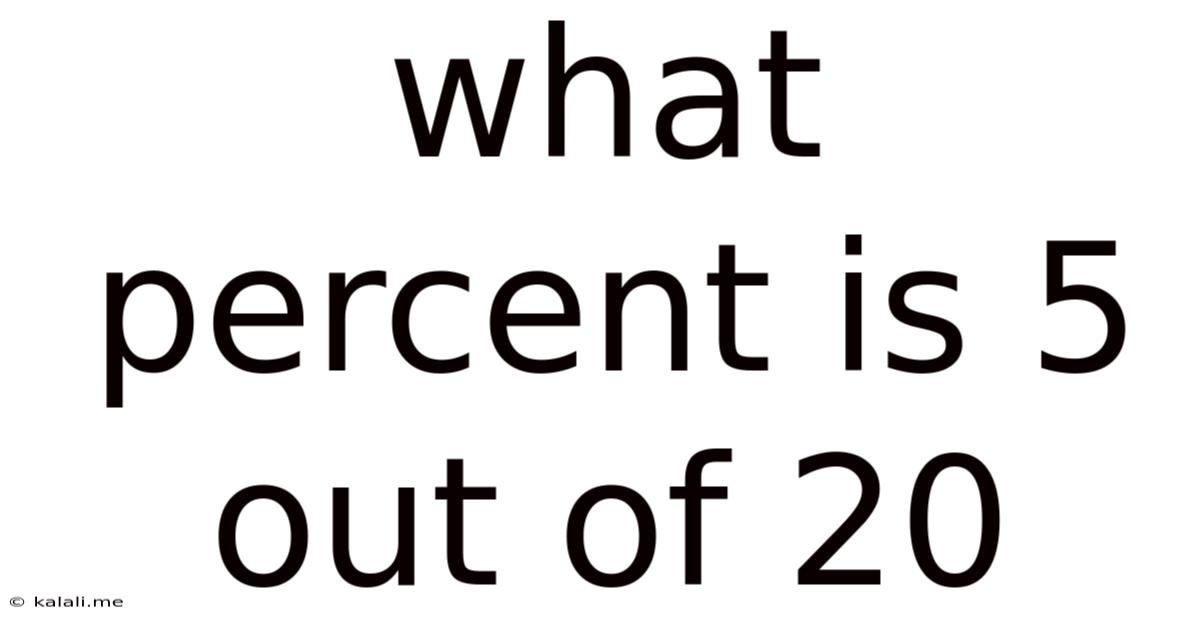
Table of Contents
What Percent is 5 out of 20? A Deep Dive into Percentages and Their Applications
Meta Description: Understanding percentages is crucial in many areas of life. This comprehensive guide explains how to calculate what percent 5 out of 20 represents, offering various methods and real-world examples to solidify your understanding. We'll delve into the fundamentals of percentages, explore different calculation approaches, and discuss practical applications across diverse fields.
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex statistical analysis. This article comprehensively explores the question, "What percent is 5 out of 20?" We'll not only provide the answer but also delve into the underlying concepts, alternative calculation methods, and real-world applications to ensure a thorough understanding of percentage calculations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ( per cent). This representation makes it easy to compare different proportions. For example, 25% means 25 out of 100, which can also be expressed as the fraction 25/100 or the decimal 0.25.
Understanding this basic definition is key to tackling any percentage problem. The ability to convert between fractions, decimals, and percentages is equally important.
Calculating "What Percent is 5 out of 20?"
There are several ways to calculate what percentage 5 represents out of 20. Let's explore the most common methods:
Method 1: Using the Fraction Method
The most straightforward method is to represent the given numbers as a fraction and then convert it to a percentage.
-
Form a fraction: Express "5 out of 20" as a fraction: 5/20.
-
Simplify the fraction (optional): To simplify the fraction, find the greatest common divisor (GCD) of the numerator (5) and the denominator (20). The GCD of 5 and 20 is 5. Divide both the numerator and the denominator by 5: 5/20 simplifies to 1/4.
-
Convert the fraction to a decimal: Divide the numerator (1) by the denominator (4): 1 ÷ 4 = 0.25
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.25 × 100 = 25%
Therefore, 5 out of 20 is 25%.
Method 2: Using Proportions
This method uses the concept of proportions to solve for the unknown percentage.
-
Set up a proportion: We can set up a proportion as follows:
x/100 = 5/20where 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiply the proportion: 20x = 500
-
Solve for x: Divide both sides by 20: x = 500 ÷ 20 = 25
Therefore, x = 25%, confirming that 5 out of 20 is 25%.
Method 3: Using the Percentage Formula
The general formula for calculating a percentage is:
(Part / Whole) × 100%
In this case:
Part = 5 Whole = 20
Applying the formula:
(5 / 20) × 100% = 0.25 × 100% = 25%
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous everyday situations and professional fields. Here are some examples:
-
Calculating Discounts: If a store offers a 20% discount on a $100 item, you can calculate the discount amount by multiplying 100 by 0.20 ($20) and subtracting it from the original price ($80).
-
Determining Grades: Academic grades are often expressed as percentages, reflecting the ratio of correct answers to total questions.
-
Analyzing Financial Statements: Businesses use percentages to analyze financial performance, such as profit margins, revenue growth, and expense ratios. Understanding these metrics is crucial for making informed business decisions.
-
Understanding Statistics: Percentages are extensively used in statistical analysis to represent proportions within datasets, allowing for easier interpretation and comparison of data. For example, unemployment rates, survey results, and population demographics are commonly presented as percentages.
-
Calculating Interest: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding interest rates is crucial for making informed financial decisions.
-
Cooking and Baking: Recipes often require adjusting ingredient quantities based on the number of servings. Percentage calculations facilitate this adjustment accurately.
-
Sports Statistics: Sports statistics heavily rely on percentages to represent various performance metrics, such as batting averages in baseball, free throw percentages in basketball, and completion percentages in American football. These percentages provide insightful comparisons between players and teams.
Beyond the Basics: More Complex Percentage Problems
While the problem "What percent is 5 out of 20?" provides a simple introduction to percentage calculations, more complex problems require a deeper understanding of the concepts involved. Here are a few examples:
-
Finding the Whole: If 15% of a number is 30, what is the number? This type of problem requires solving for the "whole" using the percentage formula.
-
Finding the Part: What is 35% of 80? This requires calculating a specific portion of a given whole.
-
Percentage Increase and Decrease: Calculating percentage change (increase or decrease) requires determining the difference between two values and expressing it as a percentage of the original value. This is crucial in tracking changes over time, such as stock prices, population growth, or inflation rates.
-
Compounding Percentages: This involves applying a percentage repeatedly to a base value, such as calculating compound interest on a savings account.
Solving these more complex problems often requires rearranging the percentage formula and employing algebraic techniques.
Conclusion: Mastering Percentages for Success
The ability to calculate percentages is a valuable skill with wide-ranging applications in personal finance, business, academics, and numerous other areas. This article demonstrated various methods for calculating percentages, providing a comprehensive understanding of the process and showcasing its practical relevance in diverse scenarios. By mastering percentage calculations, you'll enhance your problem-solving skills and develop a deeper understanding of numerical relationships in the world around you. Remember to practice regularly to improve your fluency and accuracy. As you continue to practice and explore more complex percentage problems, your confidence and expertise will grow, making you more adept at tackling various quantitative challenges.
Latest Posts
Latest Posts
-
Is A Nonmetal A Noble Gas
Apr 17, 2025
-
How Are Elements Similar From Compounds
Apr 17, 2025
-
How Many Ounces Is One Cup Of Sour Cream
Apr 17, 2025
-
What Is A 19 Out Of 21
Apr 17, 2025
-
How Many Angles Does A Trapezoid Have
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 5 Out Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.