What Percent Is 5 Out Of 25
Kalali
Apr 25, 2025 · 6 min read
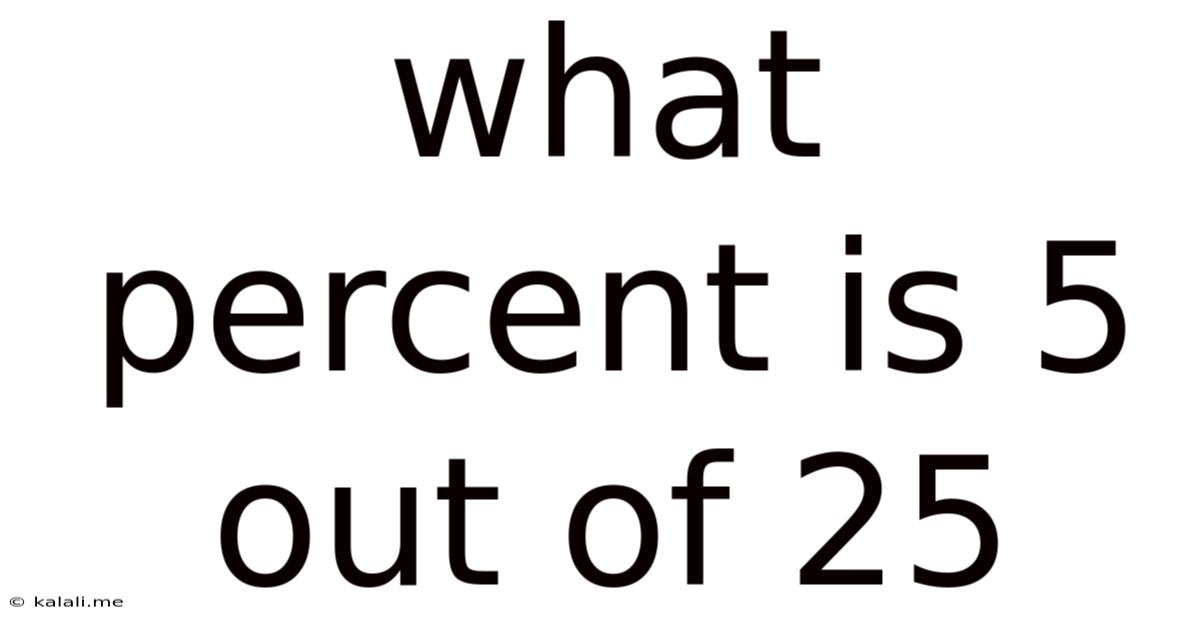
Table of Contents
What Percent is 5 out of 25? A Deep Dive into Percentages and Their Applications
What percent is 5 out of 25? The answer, a seemingly simple 20%, opens the door to a much broader understanding of percentages, their calculations, and their widespread applications in various fields. This article will not only answer the initial question but also delve into the underlying mathematical principles, explore different methods of calculation, and demonstrate real-world examples showcasing the significance of percentages.
Meta Description: This comprehensive guide explains how to calculate what percent 5 out of 25 represents, detailing various methods, real-world applications, and the underlying mathematical principles of percentage calculations.
The fundamental concept behind percentages is the representation of a fraction as a portion of 100. In simpler terms, it expresses a ratio as a number out of 100. Understanding this core concept is crucial to grasping the significance of percentages and their practical applications in daily life. The question "What percent is 5 out of 25?" essentially asks us to express the fraction 5/25 as a percentage.
Method 1: The Direct Calculation Method
The most straightforward method involves converting the fraction into a decimal and then multiplying by 100.
-
Convert the fraction to a decimal: Divide the numerator (5) by the denominator (25): 5 ÷ 25 = 0.2
-
Multiply by 100 to express as a percentage: 0.2 x 100 = 20%
Therefore, 5 out of 25 is 20%. This method is efficient and easily understandable, making it ideal for quick calculations.
Method 2: Simplifying the Fraction
This method involves simplifying the fraction before converting it to a decimal. Simplifying the fraction makes the subsequent division easier.
-
Simplify the fraction: Both 5 and 25 are divisible by 5. Simplifying the fraction 5/25 gives us 1/5.
-
Convert the simplified fraction to a decimal: 1 ÷ 5 = 0.2
-
Multiply by 100 to express as a percentage: 0.2 x 100 = 20%
This method demonstrates that simplifying fractions can often streamline the calculation process, particularly with larger numbers.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the percentage.
-
Set up a proportion: We can set up a proportion: x/100 = 5/25. Here, 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiplying gives us 25x = 500.
-
Solve for x: Divide both sides by 25: x = 20. Therefore, x = 20%, confirming our previous results.
This method highlights the relationship between fractions and percentages, offering a more algebraic approach to problem-solving.
Real-World Applications of Percentage Calculations
Percentages are ubiquitous in various aspects of daily life, from finance and business to academics and healthcare. Understanding percentage calculations is essential for making informed decisions and interpreting data effectively. Here are some examples:
-
Finance: Calculating interest rates on loans, mortgages, and savings accounts. Understanding compound interest, which involves applying percentages repeatedly, is crucial for long-term financial planning. For example, determining the percentage increase or decrease in your investment portfolio requires precise percentage calculations.
-
Business: Analyzing sales figures, profit margins, and market shares. Businesses rely heavily on percentage calculations to track their performance, assess market trends, and make strategic decisions regarding pricing, production, and marketing. For instance, calculating the percentage of defective products in a batch is critical for quality control.
-
Academics: Calculating grades, test scores, and overall performance. Students frequently encounter percentages in their academic journey, from calculating their GPA to determining their standing relative to their classmates. Understanding how percentages are used in grading systems is essential for academic success.
-
Healthcare: Determining the effectiveness of treatments, analyzing disease prevalence, and interpreting medical test results. In medicine, percentages are critical for describing the probability of outcomes, analyzing the effectiveness of medical interventions, and interpreting diagnostic data. For example, doctors might use percentages to describe the likelihood of a patient's recovery.
-
Shopping: Calculating discounts and sales tax. Consumers regularly encounter percentages when shopping, with discounts often expressed as a percentage off the original price. Understanding how to calculate the final price after a discount and sales tax is vital for budget management.
-
Data Analysis: Representing proportions, trends, and changes in data sets. Percentage changes are used to illustrate trends and compare data over time in various fields, from economics to demographics. For example, economists use percentage changes in GDP to gauge economic growth or decline.
-
Sports: Calculating batting averages, win percentages, and player statistics. In sports, percentages are essential for evaluating player performance and team success. Baseball batting averages, for example, are expressed as percentages.
Beyond the Basics: Advanced Percentage Calculations
While calculating 20% of 25 is relatively simple, more complex percentage problems may require additional steps. Let's consider some examples:
-
Finding a Percentage of a Number: Calculating 15% of 300 requires multiplying 300 by 0.15 (15/100), resulting in 45. This is a common calculation in various contexts, from determining discounts to calculating commissions.
-
Finding the Percentage Increase or Decrease: If a quantity increases from 100 to 120, the percentage increase is calculated as [(120 - 100) / 100] x 100 = 20%. Similarly, a decrease from 150 to 120 represents a [(150 - 120) / 150] x 100 = 20% decrease.
-
Calculating Percentage Change Over Time: Tracking percentage changes over multiple periods, such as analyzing year-over-year growth in a business, requires calculating the percentage change for each period and potentially averaging or compounding these changes to get an overall picture.
-
Working with Percentages in Equations: Percentages can be incorporated into more complex mathematical equations, particularly in fields like finance and statistics. For example, the present value formula or future value formula heavily utilizes percentages to determine the present and future values of an investment.
Troubleshooting Common Percentage Calculation Errors
Even seemingly simple percentage calculations can be prone to errors if not approached carefully. Some common mistakes include:
-
Incorrect Order of Operations: Following the correct order of operations (PEMDAS/BODMAS) is crucial when percentages are involved in more complex calculations. Errors often arise from incorrectly prioritizing addition, subtraction, multiplication, and division.
-
Confusing Percentage Increase and Decrease: Clearly distinguishing between percentage increase and percentage decrease is essential. The calculations differ, and incorrect application can lead to significant inaccuracies.
-
Inaccurate Decimal Conversion: Converting fractions to decimals correctly is crucial. A slight error in the decimal conversion will propagate through the entire calculation, resulting in an incorrect final answer.
-
Misinterpreting the Problem: Carefully understanding the question and identifying the relevant values is crucial. Misinterpreting the problem statement often leads to the use of incorrect values in the calculation.
Conclusion
The seemingly simple question, "What percent is 5 out of 25?" unveils a world of mathematical concepts and their practical applications. Understanding percentages is fundamental to navigating various aspects of life, from personal finances to professional success. By mastering the different methods of percentage calculation and avoiding common pitfalls, individuals can confidently tackle complex percentage problems and utilize this knowledge effectively in various real-world scenarios. The ability to accurately calculate and interpret percentages is not just a mathematical skill but a valuable tool for informed decision-making and data analysis in numerous fields.
Latest Posts
Latest Posts
-
What Percent Of 21 Is 28
Apr 25, 2025
-
What Is 30 By 40 Cm In Inches
Apr 25, 2025
-
How Many Kilograms Is 500 Grams
Apr 25, 2025
-
How Much Is 200 Oz Of Water
Apr 25, 2025
-
What Is 21 5 Cm In Inches
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 5 Out Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.