What Percent Is 6 Of 15
Kalali
Apr 28, 2025 · 5 min read
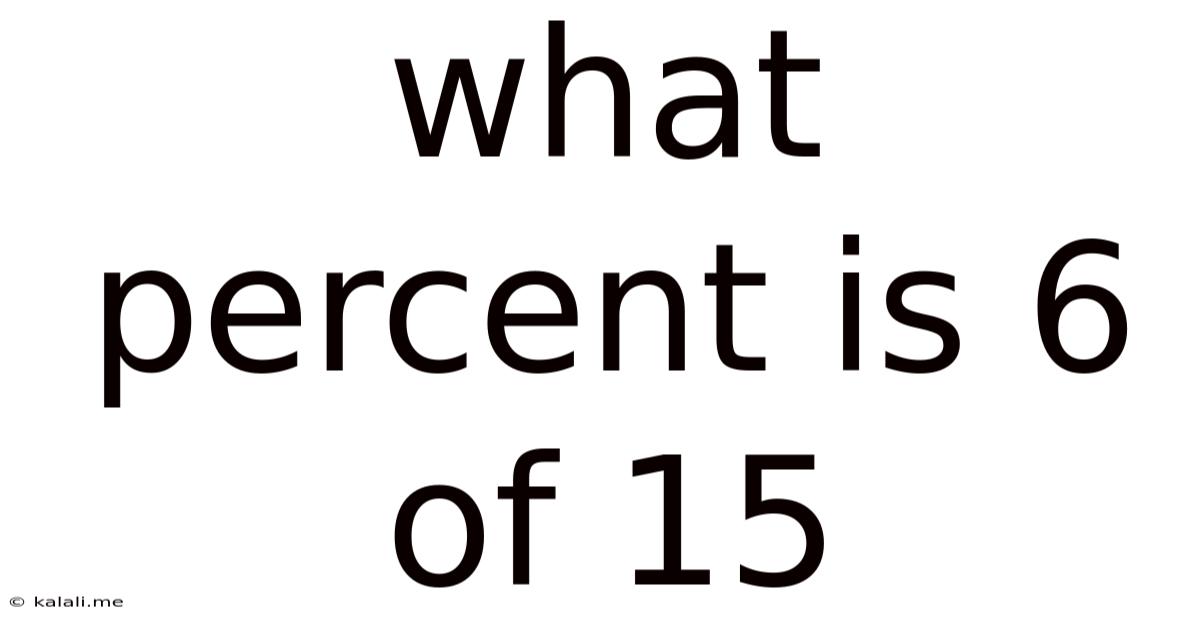
Table of Contents
What Percent is 6 of 15? A Deep Dive into Percentage Calculations and Their Applications
Meta Description: Uncover the answer to "What percent is 6 of 15?" and explore the world of percentage calculations. This comprehensive guide explains the process, provides practical examples, and delves into real-world applications of percentages. Learn how to calculate percentages, understand their significance, and master this fundamental mathematical concept.
Calculating percentages is a fundamental skill with wide-ranging applications in everyday life, from understanding sales discounts to analyzing financial reports. This article will not only answer the question, "What percent is 6 of 15?" but also delve into the broader concept of percentage calculations, exploring various methods, practical examples, and real-world applications. We'll also touch upon the importance of understanding percentages in different fields and how this knowledge can empower you to make informed decisions.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Percentages are a convenient way to express proportions and compare different quantities. Understanding percentages requires familiarity with fractions, decimals, and ratios. They are all interconnected and represent different ways of expressing the same relative value.
For instance, 50% can be represented as:
- Fraction: 50/100 (which simplifies to 1/2)
- Decimal: 0.50
Calculating "What Percent is 6 of 15?"
Now, let's tackle the core question: What percent is 6 of 15? There are several ways to approach this calculation:
Method 1: Using the Formula
The most common method involves using the percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 6
- Whole: 15
Substituting these values into the formula:
(6 / 15) x 100 = 40%
Therefore, 6 is 40% of 15.
Method 2: Simplifying the Fraction
We can also simplify the fraction 6/15 before multiplying by 100. Both 6 and 15 are divisible by 3:
6/15 simplifies to 2/5
To convert 2/5 to a percentage, we multiply by 100:
(2/5) x 100 = 40%
This method demonstrates the interconnectedness of fractions and percentages.
Method 3: Using Proportions
Another approach involves setting up a proportion:
6/15 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
15x = 600
x = 600 / 15
x = 40
Therefore, x = 40%, confirming our previous calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios:
1. Finance and Budgeting:
- Interest Rates: Understanding interest rates on loans, savings accounts, and investments requires a strong grasp of percentages.
- Financial Statements: Analyzing financial reports, such as income statements and balance sheets, involves interpreting data presented as percentages.
- Taxes: Calculating income tax, sales tax, and other taxes often involves percentage calculations.
- Discounts and Sales: Determining the final price of an item after a discount is applied necessitates understanding percentage reductions. For example, a 20% discount on a $100 item means a $20 reduction, resulting in a final price of $80.
- Investment Returns: Tracking the performance of investments, calculating returns on investment (ROI), and understanding compound interest all depend heavily on percentage calculations.
2. Retail and Sales:
- Profit Margins: Retailers calculate profit margins as a percentage of the selling price.
- Markup: Determining the selling price of an item based on the cost price and desired markup percentage.
- Sales Tax: Calculating sales tax on purchases.
- Discounts and Promotions: Offering discounts and promotions expressed as percentages to attract customers.
3. Science and Research:
- Data Analysis: Scientists use percentages to present and analyze experimental data. For example, expressing the percentage of participants in a study who experienced a particular outcome.
- Statistical Analysis: Percentages are fundamental in statistical calculations and hypothesis testing.
4. Education:
- Grades and Assessments: Grading systems often use percentages to represent student performance.
- Statistical Representation of Data: Educational research often utilizes percentages to summarize and analyze data.
5. Everyday Life:
- Tips and Gratuities: Calculating tips in restaurants involves understanding percentages.
- Surveys and Polls: Results from surveys and polls are often reported as percentages.
- Understanding Statistics: News reports, articles, and data visualizations frequently use percentages to convey information effectively.
Advanced Percentage Calculations
Beyond the basic calculations, understanding more complex percentage problems is vital. Here are some examples:
-
Percentage Increase/Decrease: Calculating the percentage change between two values. For example, if a value increases from 100 to 120, the percentage increase is 20%. The formula is:
((New Value - Old Value) / Old Value) x 100 -
Percentage of a Percentage: Calculating a percentage of a percentage. For example, finding 10% of 20% of 100. This involves sequential percentage calculations.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. It's a more complex calculation that demonstrates the power of exponential growth.
Mastering Percentages: Tips and Tricks
-
Practice Regularly: The key to mastering percentages is consistent practice. Work through various examples and problems to build your understanding and speed.
-
Use Online Calculators and Resources: Many online resources and calculators can help you verify your answers and explore different percentage calculation methods.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying concepts of fractions, decimals, and ratios. This will give you a more solid foundation for tackling more complex problems.
-
Break Down Complex Problems: When faced with a complex percentage problem, break it down into smaller, more manageable steps.
-
Check Your Work: Always check your answers to ensure accuracy. Use alternative methods to verify your calculations.
Conclusion
Understanding percentages is a valuable life skill applicable across numerous fields. This article has explored the fundamental concepts of percentage calculations, demonstrated various methods to determine "What percent is 6 of 15?", and highlighted the numerous real-world applications of this mathematical concept. By mastering percentage calculations, you equip yourself with a powerful tool for analyzing data, making informed decisions, and confidently navigating the quantitative aspects of everyday life and professional endeavors. Remember consistent practice and a solid understanding of the underlying principles are key to achieving proficiency.
Latest Posts
Latest Posts
-
4 2 5 As An Improper Fraction
Apr 28, 2025
-
How Many Meters Is 400 Ft
Apr 28, 2025
-
How Many Ft Is 50 Cm
Apr 28, 2025
-
What Is 5 And 3 8 As A Decimal
Apr 28, 2025
-
240 Ml Is How Many Cups
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 6 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.