What Percent Is 60 Of 150
Kalali
Apr 17, 2025 · 5 min read
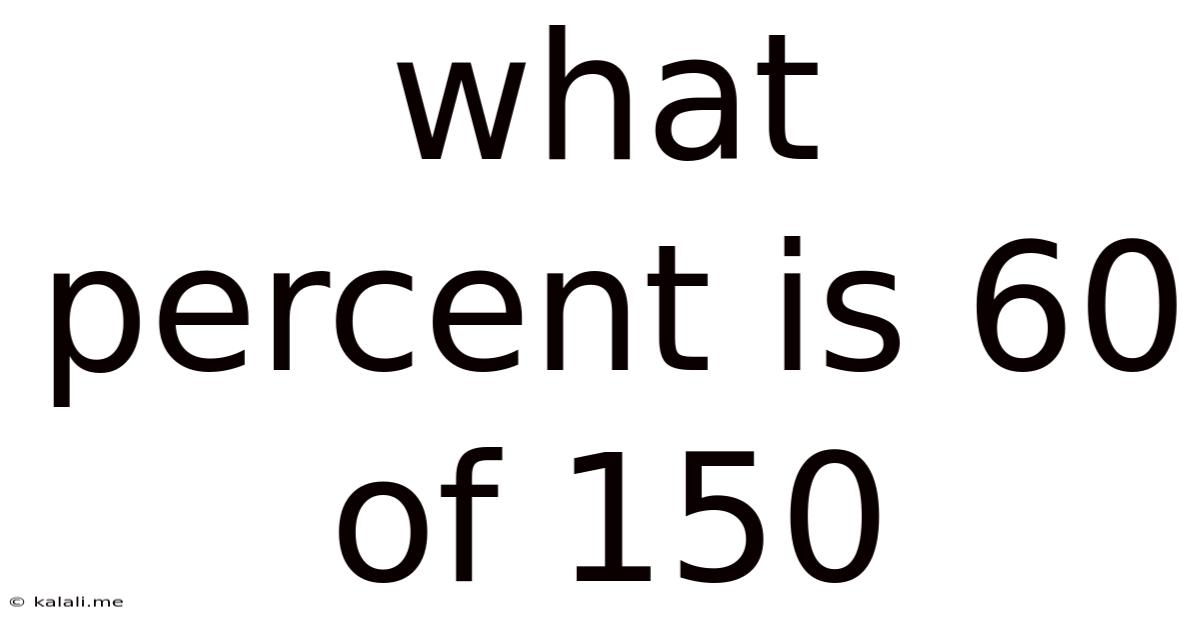
Table of Contents
What Percent is 60 of 150? A Comprehensive Guide to Percentage Calculations
This article delves into the question: "What percent is 60 of 150?" We'll not only solve this specific problem but also explore the underlying principles of percentage calculations, providing you with the knowledge and tools to tackle similar problems with confidence. Understanding percentages is crucial in various aspects of life, from everyday budgeting and shopping to more complex financial analyses and scientific applications. This guide will equip you with a thorough understanding of the subject.
Meta Description: Learn how to calculate percentages effectively! This comprehensive guide explains how to determine what percent 60 is of 150, covering fundamental percentage concepts, formulas, and practical applications. Master percentage calculations for everyday use and advanced applications.
Understanding Percentages: The Basics
A percentage is a fraction expressed as a number out of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10.
Understanding the relationship between fractions, decimals, and percentages is key to mastering percentage calculations. They are all different ways of representing the same proportion. For example:
- Fraction: 1/2
- Decimal: 0.5
- Percentage: 50%
These all represent the same value – half.
Calculating Percentages: The Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100 = Percentage
Where:
- Part: The value you want to express as a percentage of the whole.
- Whole: The total value.
- Percentage: The result expressed as a percentage.
Solving the Problem: What Percent is 60 of 150?
Now let's apply the formula to answer the question: "What percent is 60 of 150?"
In this case:
- Part: 60
- Whole: 150
Using the formula:
(60 / 150) x 100 = Percentage
-
Divide the part by the whole: 60 / 150 = 0.4
-
Multiply by 100: 0.4 x 100 = 40
Therefore, 60 is 40% of 150.
Different Approaches to Percentage Calculation
While the above formula is the most straightforward, there are alternative methods to calculate percentages, especially helpful depending on the complexity of the problem or your preference:
1. Using Proportions:
This method sets up a proportion to solve for the unknown percentage. We can represent the problem as:
60/150 = x/100
To solve for x (the percentage), we cross-multiply:
60 * 100 = 150 * x
6000 = 150x
x = 6000 / 150 = 40
Therefore, x = 40%, confirming our earlier result.
2. Using Decimal Conversion:
First, convert the fraction (Part/Whole) into a decimal:
60/150 = 0.4
Then, multiply the decimal by 100 to obtain the percentage:
0.4 * 100 = 40%
3. Using a Calculator:
Most calculators have a percentage function (%) that simplifies the calculation. Simply enter 60 ÷ 150 x 100 = and the calculator will directly provide the answer: 40%.
Practical Applications of Percentage Calculations
Percentage calculations are used extensively in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, taxes, and investment returns. For example, understanding interest rates on loans or savings accounts relies heavily on percentage calculations. Calculating the amount of discount on sale items also uses percentages.
-
Business: Analyzing sales figures, market share, growth rates, and customer satisfaction levels. Tracking key performance indicators (KPIs) often involves percentage changes.
-
Science: Representing data, expressing concentrations, and calculating statistical probabilities. In chemistry, concentrations are often expressed as percentages.
-
Everyday Life: Calculating tips in restaurants, determining discounts in stores, understanding tax rates, and even interpreting survey results. These everyday tasks frequently involve percentage calculations.
-
Education: Calculating grades, assessing test performance, and measuring student progress. Percentage scores are a standard method for evaluating academic achievement.
Advanced Percentage Calculations: Finding the Whole or the Part
The formula we've discussed so far helps find the percentage. But what if you need to find the whole or the part given the percentage and one other value? Let's explore these scenarios:
1. Finding the Whole:
If you know the percentage and the part, you can find the whole using this formula:
Whole = (Part / Percentage) x 100
For example: If 20% of a number is 40, what is the number?
Whole = (40 / 20) x 100 = 200
2. Finding the Part:
If you know the percentage and the whole, you can find the part using this formula:
Part = (Percentage / 100) x Whole
For example: What is 30% of 250?
Part = (30 / 100) x 250 = 75
Percentage Increase and Decrease
Percentage change is another vital application of percentages. It measures the relative change between an old value and a new value.
Percentage Increase:
Percentage Increase = [(New Value - Old Value) / Old Value] x 100
For example: If a price increased from $100 to $120, the percentage increase is:
Percentage Increase = [(120 - 100) / 100] x 100 = 20%
Percentage Decrease:
Percentage Decrease = [(Old Value - New Value) / Old Value] x 100
For example: If a price decreased from $150 to $120, the percentage decrease is:
Percentage Decrease = [(150 - 120) / 150] x 100 = 20%
Troubleshooting Common Percentage Calculation Errors
Several common mistakes can occur when calculating percentages:
-
Incorrect Formula: Using the wrong formula can lead to inaccurate results. Double-check the formula based on what you need to calculate (percentage, part, or whole).
-
Decimal Errors: Mistakes in decimal point placement during calculations are frequent. Carefully verify each step to ensure accuracy.
-
Order of Operations: Incorrect order of operations (PEMDAS/BODMAS) can also lead to errors. Remember to follow the correct order of operations.
-
Unit Inconsistencies: Ensure all values are in the same units. Inconsistencies in units can result in incorrect calculations.
Conclusion
Understanding percentages is a fundamental skill with broad applications in various fields. By mastering the fundamental concepts and formulas discussed in this article, you can confidently tackle a wide range of percentage problems, from simple calculations to more complex scenarios. Remember to practice regularly and always double-check your work to avoid common errors. The ability to confidently work with percentages empowers you to make informed decisions in many aspects of your life, whether personal finance, business, or everyday situations. So, go forth and confidently calculate those percentages!
Latest Posts
Latest Posts
-
What Is 2 3 8 As A Decimal
Apr 19, 2025
-
How To Tell A Chemical Reaction Has Occurred
Apr 19, 2025
-
How Much Is 23 Degrees Celsius In Fahrenheit
Apr 19, 2025
-
How Much Is 160 Celsius In Fahrenheit
Apr 19, 2025
-
How Many Pounds In 2000 Grams
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 60 Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.