What Percent Of 10 Is 6
Kalali
Apr 18, 2025 · 5 min read
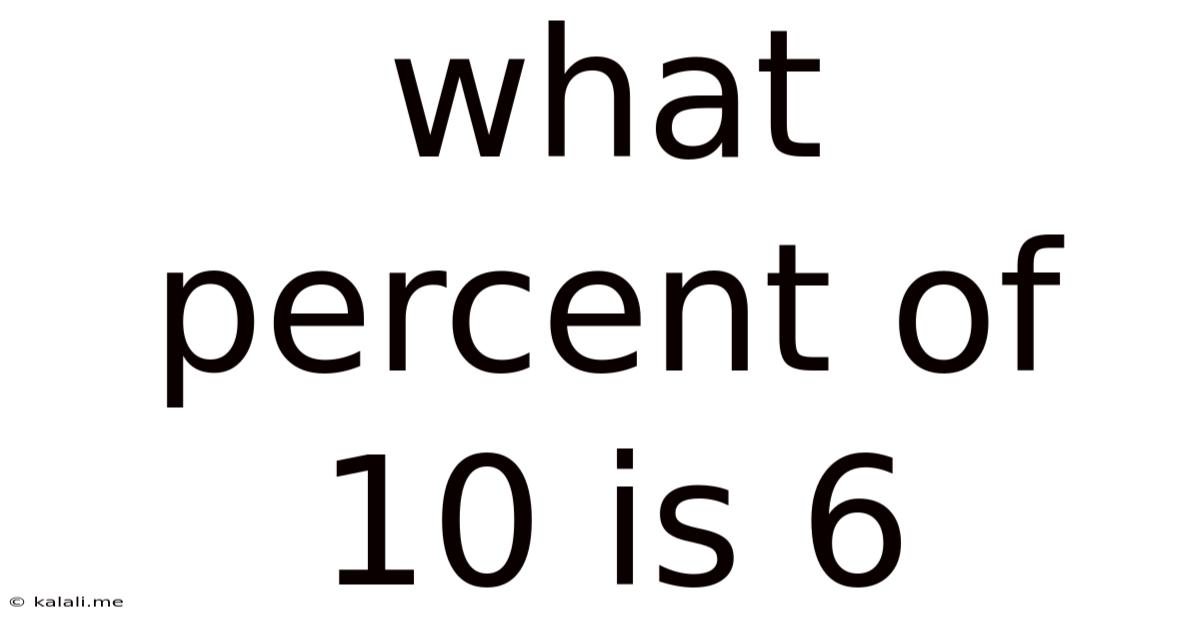
Table of Contents
What Percent of 10 is 6? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What percent of 10 is 6?", opens the door to a fascinating exploration of percentages, their practical applications, and the underlying mathematical concepts. While the answer itself is straightforward, understanding the how and why behind the calculation is crucial for navigating various scenarios in everyday life, from calculating discounts and tax rates to understanding statistical data and financial reports. This article will delve into the calculation, explain the methodology, and explore the broader context of percentage calculations.
Meta Description: Learn how to calculate what percent of 10 is 6. This comprehensive guide explains the method, explores practical applications of percentages, and provides examples for a deeper understanding of percentage calculations.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100". So, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Understanding this basic definition is key to solving percentage problems. Percentages are a powerful tool for comparing proportions, representing changes, and making sense of data.
Calculating "What Percent of 10 is 6?"
The core of the question lies in understanding the relationship between the parts and the whole. In this case, 6 is the part, and 10 is the whole. To find the percentage, we need to determine what fraction 6 represents of 10 and then convert that fraction into a percentage.
Here's the step-by-step calculation:
-
Form a fraction: Express the problem as a fraction: 6/10.
-
Convert the fraction to a decimal: Divide the numerator (6) by the denominator (10): 6 ÷ 10 = 0.6
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.6 x 100 = 60%.
Therefore, 6 is 60% of 10.
Different Approaches to Solving Percentage Problems
While the method above is straightforward, there are other ways to approach percentage calculations, particularly when dealing with more complex problems. Let's explore a few alternative methods:
-
Using proportions: This method involves setting up a proportion, equating two ratios. For instance, we can set up the proportion: x/100 = 6/10. Solving for x (the percentage) will give us the answer. Cross-multiplying, we get 10x = 600, and dividing by 10, we find x = 60%.
-
Using the percentage formula: The general formula for percentage calculations is: (Part/Whole) x 100 = Percentage. Plugging in the values from our problem, we get (6/10) x 100 = 60%.
-
Using mental math (for simpler problems): For simple problems like this, you might be able to solve it mentally. Since 6 is 6/10 of 10, and 6/10 is equivalent to 60/100, you can directly determine that it's 60%.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world situations. Here are just a few examples:
-
Sales and discounts: Calculating discounts in stores, understanding sale prices, and determining the final price after a discount. For instance, a 20% discount on a $100 item means a reduction of $20 (20% of $100), resulting in a final price of $80.
-
Taxes and interest: Calculating sales tax, income tax, or interest on loans and investments. Understanding the percentage of tax or interest helps you budget and manage your finances effectively.
-
Financial analysis: Analyzing financial statements, understanding profit margins, return on investment (ROI), and other key financial metrics. Percentage changes in revenue, expenses, or profits provide valuable insights into the financial health of a business.
-
Statistics and data analysis: Representing data in percentages makes it easier to compare and interpret. For example, understanding the percentage of people who prefer a particular product or service can help businesses make informed decisions.
-
Scientific measurements and experiments: Percentages are used extensively in scientific fields to represent concentrations, error rates, and changes in measurements.
-
Grade calculations: In education, calculating grades often involves converting scores to percentages.
Beyond the Basics: More Complex Percentage Problems
While "What percent of 10 is 6?" is a fundamental problem, understanding percentages extends to more complex scenarios. These include:
-
Finding the whole when given the part and the percentage: For example, if 25% of a number is 5, what is the number? This involves working backward using the percentage formula.
-
Calculating percentage increase or decrease: Determining the percentage change between two values. For instance, if a price increases from $50 to $60, the percentage increase is calculated as [(60-50)/50] x 100 = 20%.
-
Compound interest calculations: Calculating interest that accrues not only on the principal but also on accumulated interest. This is a more advanced application of percentages crucial in finance.
Mastering Percentages: Tips and Practice
Mastering percentages requires practice and a solid understanding of the underlying concepts. Here are some tips to improve your skills:
-
Practice regularly: Solve a variety of percentage problems, starting with simpler ones and gradually progressing to more complex scenarios.
-
Use different methods: Experiment with different approaches to solving percentage problems to find the method that suits you best.
-
Visual aids: Use visual aids like diagrams or charts to visualize the problem and understand the relationships between the parts and the whole.
-
Real-world application: Apply percentage calculations to real-life situations to solidify your understanding and improve your problem-solving skills. Try calculating discounts at the store, analyzing financial data, or figuring out the percentage of correct answers on a test.
-
Utilize online resources: Numerous online resources, including calculators and tutorials, can help you practice and improve your understanding of percentages.
In conclusion, the seemingly simple question "What percent of 10 is 6?" serves as a springboard for a comprehensive understanding of percentages. Mastering this fundamental concept unlocks a world of possibilities, equipping you with the skills to navigate numerous real-world scenarios requiring percentage calculations. From simple discounts to complex financial analysis, the ability to accurately and efficiently work with percentages is a valuable asset in various aspects of life. Remember to practice regularly and apply your knowledge to real-world problems to truly solidify your understanding.
Latest Posts
Latest Posts
-
How Many Hours Is 166 Minutes
Apr 19, 2025
-
What Is 20 Off Of 70
Apr 19, 2025
-
25 Is What Percent Of 65
Apr 19, 2025
-
How Many Ounces In 2 1 2 Quarts
Apr 19, 2025
-
17 Is What Percent Of 68
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 10 Is 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.